Cách giải §5. Trường hợp đồng dư thứ nhất, Chương 3 – Tam giác đồng dạng, SGK Toán 8, tập 1, tr. Nội dung Giải bài 29 30 31 trang 74 75 SGK Toán 8 tập 2 bao gồm các công thức, lý thuyết và các phương pháp giải bài tập hình học trong SGK Toán 8 giúp các em học tốt Toán lớp 8.
Lý thuyết
Lý thuyết
Hai tam giác bằng nhau nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia.
$\delta abc, \delta a’b’c’:\,\ \frac{a’b’}{ab}=\frac{a’c’}{ac}= \frac{b’c’}{bc}\rightarrow \delta abc\sim \delta a’b’c’$
Sau đây là hướng dẫn trả lời bài học này để các bạn tham khảo. Vui lòng đọc kỹ câu hỏi trước khi trả lời!
Câu hỏi
1. Trả lời câu 1 trang 73 sgk toán 8 tập 2
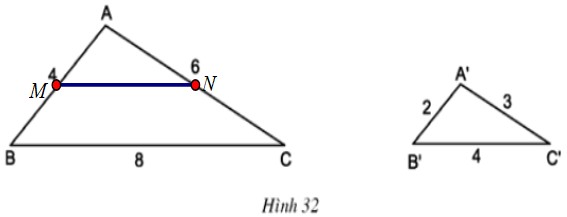
Các kích thước của hai hình tam giác \(abc\) và \(a’b’c’\) được thể hiện trong Hình 32 (cùng đơn vị đo là centimet)
Lấy hai điểm \(m, n\) thuộc hai cạnh \(ab\) và \(ac\) của tam giác \(abc\), sao cho
\(am = a’b’ = 2cm; an = a’c’ = 3cm\).
Tính độ dài đoạn thẳng \(mn\).
Em có nhận xét gì về mối quan hệ giữa tam giác \(abc, amn, a’b’c’\)?
Trả lời:
Ta có:
\(\dfrac{{am}}{{ab}} = \dfrac{{an}}{{ac}} = \dfrac{1}{2}\)
\(⇒ mn // bc\) (định lý đảo ngược)
\(\eqalign{& \rightarrow {{am} \over {ab}} = {{an} \over {ac}} = {{mn} \over {bc}} = {1 \trên 2} \cr & \rightarrow mn = {1 \trên 2}bc = {1 \trên 2}.8 = 4 \,cm\cr} \)
Nhận xét: \(Δamn\) tương tự như \(Δabc\); \(Δamn = Δa’b’c’\); \(Δabc\) tương tự như \ (Δa ‘b’c’\).
2. Trả lời câu 2 trang 74 sgk toán 8 tập 2
Tìm các cặp tam giác đồng dạng trong Hình 34:
Trả lời:
Ba cạnh\(Δabc\) tỉ lệ với ba cạnh\(Δdfe\)
\(\left( {\dfrac{{ab}}{{df}} = \dfrac{{ac}}{{de}} = \dfrac{{ef}}{{bc ) }} = \dfrac{1}{2}} \right)\)
\(⇒ Δabc\) tương tự như \(Δdfe\)
Dưới đây là lời giải câu hỏi 2 SGK Toán 8 tập 29 30 31 trang 74 75. Các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn lời giải đầy đủ phần bài tập Hình học 8 và lời giải chi tiết trang 29 30 31 trang 74 75 SGK Toán Tập 2 Bài 5. Trường hợp đồng dạng thứ nhất trong Chương 3 – Tam giác đồng dạng dành cho các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 29 trang 74 sgk toán 8 tập 2
Các kích thước của các hình tam giác \(abc\) và \(a’b’c’\) được thể hiện trong Hình 35.
a) Các tam giác \(abc\) và \(a’b’c’\) có bằng nhau không? Tại sao?
b) Tính tỉ số chu vi của hai tam giác.
Giải pháp thay thế:
a)Chúng tôi có:
\(\begin{array}{l} \dfrac{{ab}}{{a’b’}} = \dfrac{6}{4} = \dfrac{3}{2 };\,\,\dfrac{{ac}}{{a’c’}} = \dfrac{9}{6} = \dfrac{3}{2};\\ dfrac{{bc}}{{b’c’}} = \dfrac{{12}}{8} = \dfrac{3}{2}\\ \rightarrow \dfrac{{ab }}{{a’b’}} = \dfrac{{ac}}{{a’c’}} = \dfrac{{bc}}{{b’c’}} = \dfrac{3 }{2} \end{array}\)
\(\rightarrow \delta abc \text{same}\delta a’b’c’\) \(\left( c-c-c \right)\)
b) Áp dụng các tính chất của chuỗi hình học:
\(\dfrac{{ab}}{{a’b’}} = \dfrac{{ac}}{{a’c’}} = \dfrac{{bc}}{{ b’c’}}\)
\(= \dfrac{{ab + ac + bc}}{{a’b’ + a’c’ + b’c’}}\) \( = \dfrac{{{ c_{abc}}}}{{c_{a’b’c’}}}} = \dfrac{3}{2}\)
2. Giải bài 30 trang 75 SGK Toán 8 Tập 2
Tam giác \(abc\) có độ dài các cạnh \(ab = 3cm, ac = 5cm, bc = 7cm\). Tam giác \(a’b’c’\) đồng dạng với tam giác \(abc\) và có chu vi bằng \(55 cm\).
Tính độ dài cạnh của \(a’b’c’\) (làm tròn đến chữ số thập phân thứ hai).
Giải pháp thay thế:
\( \rightarrow \delta abc \) giống như \( \delta a’b’c’\left( {gt} \right)\)
Áp dụng tính chất của chuỗi hình học, ta có:
\(\dfrac{{ab}}{{a’b’}} = \dfrac{{ac}}{{a’c’}} = \dfrac{{bc}}{{ b’c’}}\)\(\, = \dfrac{{ab + ac + bc}}{{a’b’ + a’c’ + b’c’}}\ ) ( = \dfrac{{{c_{abc}}}}{{{c_{a’b’c’}}}}\)
Hoặc \(\dfrac{3}{a’b’}\) = \(\dfrac{7}{b’c’}\) = \(\dfrac{5 {a’c’}\) = \(\dfrac{c_{abc}}{55}\) = \(\dfrac{3 + 7 + 5}{55}\) = (\dfrac{{15}}{{55}}\) = \(\dfrac{3}{11}\)
\( + )\,\,\dfrac{3}{{a’b’}} = \dfrac{3}{{11}}\)\(\; rightarrow a’b’ = \dfrac{{3.11}}{3} = 11\,cm\)
\( + )\,\,\dfrac{7}{{b’c’}} = \dfrac{3}{{11}}\)\(\; rightarrow b’c’ = \dfrac{{7.11}}{3} = 25,67\,cm\)
\( + )\,\,\dfrac{5}{{a’c’}} = \dfrac{3}{{11}}\)\(\; rightarrow a’c’ = \dfrac{{5.11}}{3} = 18,33\,cm\)
3. Giải bài 31 trang 75 SGK Toán 8 Tập 2
Cho hai tam giác đồng dạng có chu vi \(\dfrac{15}{17}\) và hiệu độ dài tương ứng \(12,5 cm\ ). Tính toán hai bên.
Giải pháp thay thế:
Giả sử rằng \(Δa’b’c’\) tương tự như \(Δabc\), thì \(a’b’\) và \(ab ) là\ (12,5cm\).
Vì \(Δa’b’c’\) đồng dạng với \(Δabc\) (giả sử) nên ta có:
\(\dfrac{{a’b’}}{{ab}} = \dfrac{{b’c’}}{{bc}} = \dfrac{{c’a’} {{ca}} \)\(\,= \dfrac{{a’b’ + b’c’ + c’a’}}{{ab + bc + ca}}\) (\, = \dfrac{{{c_{a’b’c’}}}}{{{c_{abc}}}} = \dfrac{{15}}{{17}}\ ) (Tính chất của chuỗi hình học).
\(\eqalign{ & \rightarrow {{ab} \over {a’b’}} – 1 = {{17} \over {15}} – 1 \cr & \rightarrow {{ab – a’b’} \over {a’b’}} = {{17 – 15} \over {15}} \cr & \rightarrow {{12,5} \vượt {a’b’}} = {2 \vượt {15}} \cr} \)
\( \rightarrow a’b’ = \dfrac{{15}}{2}.12,5 = 93,75\,cm\)
Có: \(ab – a’b’ = 12,5\,cm\)
\(\rightarrow ab = 12,5 + 93,75 = 106,25\,\,cm.\)
Trước:
- Bài tập: Giải bài 26 27 28 SGK Toán 8 trang 72
- SGK Toán 8 Tập 2 32 33 34 Trang 77
- Câu hỏi khác 8
- Học tốt vật lý lớp 8
- Học tốt môn sinh học lớp 8
- Học tốt ngữ văn lớp 8
- Điểm tốt môn lịch sử lớp 8
- Học tốt môn địa lý lớp 8
- Học tốt tiếng Anh lớp 8
- Học tốt môn tiếng Anh lớp 8 thí điểm
- Học Tin học lớp 8
- Học chăm chỉ môn gdcd lớp 8
Tiếp theo:
Xem thêm:
<3
“Môn thể thao nào đã khó giabaisgk.com”
