bài 40 trang 73 sgk toán 7 tập 2
Tam giác cân tại a của tam giác abc. Gọi g là trọng tâm, i là một điểm nằm trong tam giác và cách đều các cạnh của tam giác. Chứng minh ba điểm a, g, i thẳng hàng
Mô tả:
Giao điểm của bg và ac được gọi là m;
cg trong đó ab là n
Vì g là trọng tâm của abc
Vậy bm, cn, là trung tuyến
Nếu không thì abc nằm trong a
do bm = cn
Ta có gb = \(\frac{1}{2}\)bm; gc = \(\frac{2}{3}\)cn (t/c trọng tâm tam giác )
nhưng bm = cn nên gb = gc
Do đó: Δagb = Δagc (c.c.c)
=> \(\widehat{bag}= \widehat{cag}\) => g thuộc tia phân giác của \(\widehat{bac}\)
Δabi = aci (c.c.c)
=> \(\widehat{bai}= \widehat{cai}\) =>Ta thuộc tia phân giác của \(\widehat{bac}\)
Vì g, i là tia phân giác của \(\widehat{bac}\) nên a, g, i thẳng hàng
Bài 41 Trang 73 SGK Toán 7 Tập 2
Khoảng cách từ trọng tâm đến ba cạnh của tam giác đều có bằng nhau không? Tại sao?
Mô tả:
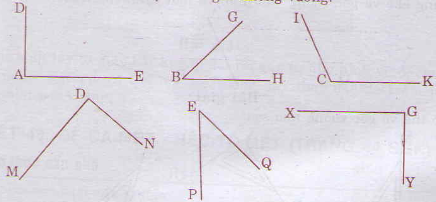
Trọng tâm của một tam giác đều cách đều các cạnh của nó:
Giả sử trọng tâm của abc là g
=> ga = \(\frac{2}{3}\)an; gb = \(\frac{2}{3}\)bm; gc = \(\ frac{2}{3}\)ec
Vì abc bằng nhau nên 3 trung tuyến an, bm, ce cũng bằng nhau
=>ga = gb = gc
Do đó: Δamg = Δcmg (c.c.c)
=> \(\widehat{amg}=\widehat{cmg}\)
\(\widehat{amg}=\widehat{cmg}\) = 1800
=> \(\widehat{amg}\) = 900
=> gm ac là khoảng cách gm từ g đến ac
Cũng chứng minh rằng ge, gn là khoảng cách từ g đến ab, ac
gm =\(\frac{1}{3}\)bm; gn = \(\frac{1}{3}\)an; ví dụ = \(\frac { 1}{3}\)ec
và an = bm = ec nên gm = gn = ge
Hoặc g cách đều các cạnh của tam giác abc
bài 42 trang 73 sgk toán 7 tập 2
Chứng minh định lý: Nếu một tam giác có một đường trung tuyến và một đường phân giác thì tam giác cân
Gợi ý: Trong Δabc, nếu ad vừa là đường trung tuyến vừa là đường phân giác thì kéo dài ad thêm ad1 sao cho da1 = ad
Mô tả:
Giả sử tia phân giác của Δabc là ad \(\widehat{bac}\) và db = dc, ta chứng minh rằng Δabc bằng nhau tại a
Đoạn quảng cáo mở rộng da1 = quảng cáo
Ta có: Δadc = Δa1dc (c.g.c)
Phải là \(\widehat{bad}= \widehat{ca_{1}d}\)
Đó \(\widehat{bad}= \widehat{cad}\) (gt)
=> \(\widehat{cad}= \widehat{ca_{1}d}\)
=> ∆aca1 trọng lượng tại c
Ta lại có: ab = a1c ( ∆adb = ∆a1dc)
ac = a1c (aca1 có trọng số là c)
=>ab = ac
Vậy abc nằm trong
Tức là: nếu một tam giác có một đường trung tuyến và một đường phân giác thì tam giác đó cân
bài 43 trang 73 sgk toán 7 tập 2
Đố vui: Hai con đường cắt nhau ở hai điểm khác nhau và cùng chảy qua một dòng sông.
Tìm địa điểm dựng đài quan sát cách đều hai bên đường và bờ sông. Có bao nhiêu vị trí?
Mô tả:
Hai con đường cắt nhau và giao nhau với một con sông tạo thành tam giác abc. Vị trí đặt trạm kiểm lâm thỏa mãn bài toán phải là giao điểm i của ba đường phân giác trong của tam giác abc và giao điểm k ad của các đường phân giác của góc a của tam giác và hai đường phân giác góc ngoài của tam giác các đỉnh d và e.
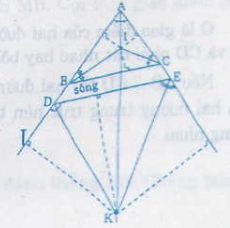
Vậy vị trí và khoảng cách ngắn nhất để dựng trạm kiểm lâm là i,k
giaibaitap.me
