Bài 12 Chương 1: Giải bài 67, 68, 69 trang 31; bài 70,71,72,73,74 trang 32 sgk toán 8 tập 1: chia một có sắp xếp – đa thức biến và cách luyện tập.
Ta thực hiện phép chia tương tự như phép chia số tự nhiên. Với hai đa thức a và b một biến b ≠ 0 thì tồn tại duy nhất hai đa thức q và r sao cho:
a = b. q + r, r = 0 hoặc thứ tự nhỏ hơn 1
– Nếu r = 0 thì chia hết.
– Nếu r bằng 0, chúng ta có thể chia cho phần còn lại.
Giải bài tập trang 31, 32 SGK Toán 12 Tập 1
Sau 67. Sắp xếp đa thức theo lũy thừa giảm dần của biến, rồi chia:
a) (x3 – 7x + 3 – x2): (x – 3);
b) (2×4 – 3×2 – 3×2 – 2 + 6x): (x2 – 2).
HD: a) (x3 – 7x + 3 – x2) : (x – 3)
Sắp xếp lại: (x3 – x2 – 7x + 3 ) : (x – 3)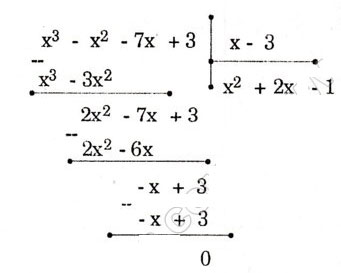
b) (2×4 – 3×2 – 3×2 – 2 + 6x): (x2 – 2)
Sắp xếp lại: (2×4 – 3×2 – 3×2 + 6x – 2) : (x2 – 2)
Bài 68. Áp dụng hằng đẳng thức dễ nhớ để thực hiện phép chia:
a) (x2 + 2xy + y2): (x + y);
b) (125×3 + 1): (5x + 1);
Xem Thêm: Cách vẽ con gà
c) (x2 – 2xy + y2) : (y – x).
HD: a) (x2 + 2xy + y2) : (x + y) = (x + y)2 : (x + y) = x + y.
b) (125×3 + 1) : (5x + 1) = [(5x)3 + 1] : (5x + 1)
= (5x)2 – 5x + 1 = 25×2 – 5x + 1.
c) (x2 – 2xy + y2) : (y – x) = (x – y)2 : [-(x – y)] = – (x – y) = y – x
Hay (x2 – 2xy + y2) : (y – x) = (y2 – 2xy + x2): (y – x)
= (y – x)2 : (y – x) = y – x.
Câu 69.Cho hai đa thức a = 3×4 + x3 + 6x – 5 và b = x2 + 1. Tìm phần dư r của phép chia a cho b và viết a = b.q + r .
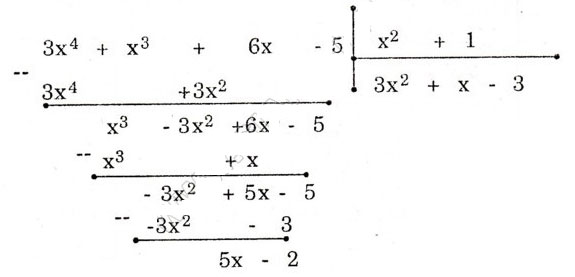
Vậy 3×4 + x3 + 6x – 5 = (x2+1)(3×2 + x – 3) + 5x – 2
Bài tập
Sau những năm 70 Bộ phận:
a) (25×5 – 5×4 + 10×2): 5×2;
b) (15x3y2 – 6x2y – 3x2y2) : 6x2y.
a) (25×5 – 5×4 + 10×2) : 5×2 = (25×5 : 5×2 ) – (5×4 : 5×2 ) + (10×2 : 5×2 ) = 5×3 – x2 + 2
b) (15x3y2 – 6x2y – 3x2y2): 6x2y
Xem Thêm: Tranh tùng hạc diên niên mang nhiều ý nghĩa trong phong thủy
= (15x3y2 : 6x2y) + (- 6x2y : 6x2y) + (- 3x2y2 : 6x2y)
= 15/6xy – 1 – 3/6y = 5/2xy – 1/2y – 1.
bài 71. Thay vì chia hết, hãy kiểm tra xem đa thức a có chia hết cho đa thức b hay không.
a) a = 15×4 – 8×3 + x2
b = 1/2×2
b) a = x2 – 2x + 1
b = 1 – x
HD: a) Ta có 15×4;8×3;x2 chia hết cho 1/2×2 nên đa thức a chia hết cho b.
b) a chia hết cho b vì x2 – 2x + 1 = (1 – x)2 chia hết cho 1 – x
bài 72 toán 8 tập 1.Phép chia:
(2×4 + x3 – 3×2 + 5x – 2): (x2 – x + 1).
Khi đó: (2×4 + x3 – 3×2 + 5x – 2) = (x2 – x + 1)(2×3 + 3x – 2).
Sau năm 73.Tính nhanh:
a) (4×2 – 9y2): (2x – 3y); b) (27×3 – 1): (3x – 1);
Xem Thêm: Tiểu cảnh mini để bàn làm việc mang lại tài lộc, may mắn
c) (8×3 + 1) : (4×2 – 2x + 1); d) (x2 – 3x + xy -3y) : (x + y)
Đáp án:a) (4×2 – 9y2) : (2x – 3y) = [(2x)2 – (3y)2] : (2x – 3y) = (2x -3y) ( 2x +3y): (2x -3y) = 2x + 3y;
b) (27×3 – 1) : (3x – 1) = [(3x)3 – 1] : (3x – 1) = (3x – 1) [(3x)2 + 3x + 1] : (3x – 1) = 9×2 + 3x + 1
c) (8×3 + 1) : (4×2 – 2x + 1) = [(2x)3 + 1] : (4×2 – 2x + 1)
= (2x + 1)[(2x)2 – 2x + 1] : (4×2 – 2x + 1)
= (2x + 1)(4×2 – 2x + 1) : (4×2 – 2x + 1) = 2x + 1
d) (x2 – 3x + xy -3y): (x + y)
= [(x2 + xy) – (3x + 3y)] : (x + y)
= [x(x + y) – 3(x + y)] : (x + y)
= (x + y)(x – 3) : (x + y)
= x – 3.
Sau 74.Tìm số a sao cho đa thức 2×3 – 3×2 + x + a chia hết cho đa thức x + 2
Giải pháp 74:
Khi đó 2×3 – 3×2 + x + a = (x + 2)(2×2 – 7x + 15) + a – 30 sao cho đa thức 2×3 – 3×2 + x + a chia hết cho đa thức (x + 2), thì phần dư của phân số a – 30 = 0 hoặc a = 30.
