Bài 20 Trang 115 – SGK Toán 7 Tập 1
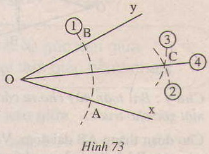
Đối với góc \(phép quay\) (h.73), vẽ một cung có tâm \(o\) và thứ tự giao điểm của \(ox, oy\) là \(a ,b\) (1). Vẽ các cung có tâm \(a\) và đường tròn tâm \(b\) có cùng bán kính sao cho chúng cắt nhau tại điểm \(c\) nằm trong góc \(quay\) ( ( 2 ) (3)).Nối \(o\) với \(c\) (4). Chứng minh rằng \(oc\) là tia phân giác của góc \(xoay chiều\).
Người chiến thắng:
Vẽ cung lấy \(o\) làm tâm, cung này cắt \(ox,oy\) tại \(a,b\) nên\(oa =ob ) vì bán kính cung tròn như nhau
Bán kính của đường tròn có tâm \(a\) và tâm đường tròn là \(b\) bằng nhau nên ta gọi bán kính là \(r\)
\(c\) là giao điểm của 2 cung nên \(c\) thuộc tâm đường tròn\(a\) nên \(ac=r\), \( c ) thuộc cung có tâm là \(b\) nên \(bc=r\)
Suy ra \(ac=bc\)
Kết nối \(bc, ac\).
Xét \(Δobc\) và \(Δoac\) có:
+)\(ob=oa\)
+)\(bc=ac\)
+) \(oc\) cạnh chung
Xem Thêm: Tiểu cảnh mini để bàn làm việc mang lại tài lộc, may mắn
Suy ra \(Δobc = Δoac(c.c.c)\)
Phải là \(\widehat{boc}=\widehat{aoc}\) (hai góc tương ứng)
Vậy \(oc\) là tia phân giác của góc \(phép quay\).
Bài 21 Trang 115 – SGK Toán 7
Cho tam giác abc, dùng thước kẻ và compa vẽ các đường phân giác của các góc a, b, c.
Người chiến thắng:
Vẽ tia phân giác của góc a.
Vẽ một cung có tâm là a. Cung này cắt ab và ac tại m và n.
Vẽ các cung tròn có tâm m và n có cùng bán kính sao cho chúng cắt nhau tại điểm i nằm trong góc bac.
Nối ai ta được tia phân giác của góc a.
Tương tự cách vẽ tia phân giác của góc b và góc c (học sinh vẽ)
Bài 22 Trang 115 – SGK Toán 7
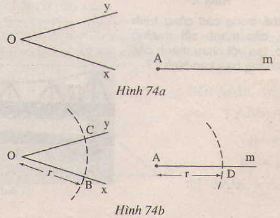
Cho góc \(phép quay\) và tia \(am\) (h.74a)
Vẽ một cung có tâm \(o\) là bán kính \(r\) và cung này sẽ cắt với \(ox,oy\) tại \(b,c )
Xem Thêm: Những hình ảnh tạm biệt đẹp nhất
Vẽ một cung có tâm \(a\) là bán kính \(r\) cắt một cung khác \(am\) tại \(d\) (h. 74b).
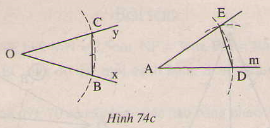
Vẽ một cung có tâm \(d\) và bán kính \(bc\), liên quan đến đường tròn có tâm \(a\) và bán kính \(r\) Cắt nhau tại \ (e\) (h. 74c).
Bằng chứng: \(\widehat{dae}=\widehat{swivel}.\)
Người chiến thắng:
Xét \(\delta dae\) và \(\delta boc\) có:
+)\(ad=ob(=r)\)
+)\(de=bc\) (gt)
+)\(ae=oc(=r)\)
Suy ra \(∆ dae= ∆ boc\;(c.c.c)\)
Suy ra \(\widehat{dae}=\widehat{boc}\) (hai góc tương ứng)
\(\widehat{boc}=\widehat{spin}.\)
Do đó: \(\widehat{dae}=\widehat{swirl}.\) (phải chứng minh)
Xem Thêm: Thuật ngữ là gì? Cho ví dụ và bài tập về thuật ngữ lớp 9
Bài 23 Trang 116 – SGK Toán 7
Đối với đoạn thẳng \(ab\)dài\(4cm\), vẽ tâm \(a\) bán kính\(2cm\) và tâm đường tròn\(b ) bán kính\( 3cm\), chúng cắt nhau tại \(c\) và \(d\), chứng minh rằng \(ab\) là một góc\ (cad\ )
Người chiến thắng:
Vì \(c\) là giao điểm của tâm đường tròn \(a\) và tâm đường tròn \(b\) nên\(ac=2cm,bc=3cm )
Vì \(d\) là giao điểm của tâm \(a\) và tâm \(b\) nên\(ad=2cm,bd=3cm\)
Do đó \(ac=ad,bc=bd\)
Xét \(Δbac\) và \(Δbad\) có:
+)\(ac=advertisement\)
+)\(bc=bd\)
+) \(ab\) cạnh chung.
Suy ra \(∆ bac= ∆ xấu(c.c.c)\)
Suy ra \(\widehat{bac}\) = \(\widehat{bad}\) (hai góc tương ứng)
Vậy \(ab\) là tia phân giác của góc \(cad\).
giaibaitap.me
Khôi phục bài viết từ Wayback Machine
