Giải bài 1, 2, 3, 4 trang 104 Sách giáo khoa Hình học 11

Bài 1 Trang 104 SGK Hình học 11

Bạn Đang Xem: Giải bài 1, 2, 3, 4 trang 104 Sách giáo khoa Hình học 11

Cho hai đường khác nhau \(a,b\) và mặt phẳng \((\alpha)\). Những câu sau đây là đúng hay sai?

a) Nếu \(a//(\alpha)\) và \(b\bot (\alpha)\) thì \(a\bot b\)

b) Nếu \(a//(\alpha)\) và \(b\bot a\) thì \(b\bot (\alpha)\)

c) Nếu \(a//(\alpha)\) và \(b// (\alpha)\) thì \(b//a\)

d) Nếu \(a\bot (\alpha)\) và \(b\bot a\) thì \(b// (\alpha)\)

NGƯỜI CHIẾN THẮNG

a) là

b) lỗi

c) lỗi

d) là sai.

bài giảng 2 trang 104 SGK Hình Học 11

Cho tứ diện \(abcd\) \(abc\) và \(bcd\) có hai mặt là hai tam giác cân có đáy chung là \(bc\). Gọi \(i\) là trung điểm của cạnh \(bc\).

a) Chứng minh rằng \(bc\) vuông góc với mặt phẳng \(adi\).

Xem Thêm: Xe Đạp Touring Là Gì Và Những Ưu Nhược Điểm Của Xe Đạp Touring

b) Gọi \(ah\) là chiều cao của tam giác \(adi\) để chứng minh rằng \(ah\) vuông góc với mặt phẳng \(bcd\).

NGƯỜI CHIẾN THẮNG

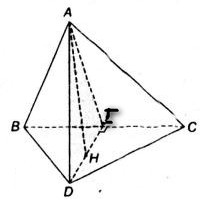
a) Tam giác \(abc\) cân tại \(a\) nên ta có đường trung trực và chiều cao tương ứng với đáy nên: \(ai\bot bc )

Xem Thêm : Bảng Tuần Hoàn Các Nguyên Tố Hóa Học: Cách Học Và Mẹo Ghi

Tương tự ta có: \(di\bot bc\)

Ta có:

$$\ còn lại. \matrix{ai \bot bc \hfill \cr di \bot bc \hfill \cr ai \cap di = {\rm{\{ }}i{\rm{\ } }} \hfill \cr} \right\} \rightarrow bc \bot (adi)$$

b) Ta có \(ah\) là chiều cao của tam giác \(adi\) nên \(ah\bot di\)

Mặt khác: \(bc\bot (adi)\) mà \(ah\subset (adi)\) phải là \(ah\bot bc\)

Chúng tôi có

$$\ còn lại. \matrix{ah \bot bc \hfill \cr ah \bot di \hfill \cr bc \cap di = {\rm{\{ }}i{\rm{\ } }} \hfill \cr} \right\} \rightarrow ah \bot (bcd)$$

Bài 3 Trang 104 SGK Hình học 11

Đối với hình chóp \(s.abcd\), đáy của nó là hình thoi \(abcd\) và có \(sa=sb=sc=sd\).gọi \(o \ ) là giao điểm của \(ac\) và \(bd\). Bằng chứng:

a) Đường thẳng \(so\) vuông góc với mặt phẳng \((abcd)\);

Xem Thêm: Bảng “tần số” các giá trị của dấu hiệu

b) Đường thẳng \( ac\) vuông góc với mặt phẳng \((sbd)\) Đường thẳng \(bd\) vuông góc với mặt phẳng \(sac\) .

NGƯỜI CHIẾN THẮNG

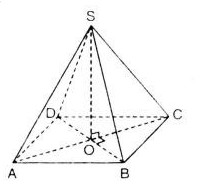
a) Theo giả thiết \(sa=sc\) tam giác \(sac\) cân tại \(s\)

\(o\) là giao điểm của hai đường chéo hình bình hành nên \(o\) là trung điểm của \(ac\) và \(bd\).

Vậy \(so\) là đường trung tuyến và chiều cao trong tam giác \(sac\) hay \(so\bot ac\) (1)

Chúng tôi nhận được bằng chứng tương tự: \(so\bot bd\) (2)

Suy ra \(so\bot (abcd)\) từ (1) và (2).

b) \(abcd\) là hình thoi nên \(ac\bot bd\) (3)

Xem Thêm : Đặc điểm, nguồn gốc và ý nghĩa đặc biệt của hoa tuyết mai

Suy ra \(ac\bot (sbd)\) từ (1) và (3)

Suy ra \(bd\bot (sac)\) từ (2) và (3)

Bài 4 Trang 105 SGK Hình học 11

Cho ba cạnh \(oa, ob, oc\) nhân đôi một tứ diện vuông góc \(oabc\). Gọi \(h\) là chân đường vuông góc kẻ từ \(o\) với mặt phẳng \((abc)\). Bằng chứng:

a) h là trọng tâm của tam giác \(abc\);

Xem Thêm: Soạn bài Bài toán dân số | Soạn văn 8 hay nhất – VietJack.com

b) \(\frac{1}{oh^{2}}=\frac{1}{oa^{2}}+\frac{1}{ob^{2}}+ \frac{1}{oc^{2}}.\)

Hướng dẫn.

(h.3.32)

a) \(h\) là hình chiếu của \(o\) trên mp \((abc)\), nên \(oh ⊥ (abc) \rightarrow oh ⊥ bc ).(1)

Ngược lại: \(oa ⊥ ob\), \(oa ⊥ oc\)

\(\rightarrow oa (obc) \rightarrow oa bc\) (2)

Suy ra \(bc ⊥ (aoh) \rightarrow bc ⊥ ah\) từ (1) và (2). Chứng minh tương tự, ta được \(ab ⊥ ch \)

\(\rightarrow h\) là trọng tâm của tam giác \(abc\).

b) Gọi \(e = ah ∩ bc\), \(oh ⊥ (abc)\), \(ae ⊂ (abc) trong mặt phẳng \((abc)\) \rightarrow oh ⊥ ae\) tại \(h\);

\(oa ⊥ (abc), oe ⊂ (abc) \rightarrow oa oe oe\) tức là \(oh\) là chiều cao của tam giác vuông \(oae\).

Ngược lại \(oe\) là chiều cao của tam giác vuông \(obc\)

Do đó: \(\frac{1}{oh^{2}}=\frac{1}{oa^{2}}+\frac{1}{oe^{2}} = \frac{1}{oa^{2}}+\frac{1}{ob^{2}}+\frac{1}{oc^{2}}.\)

Lưu ý: Biểu thức này là phần mở rộng của công thức tính chiều cao cạnh huyền của một tam giác vuông: \(\frac{1}{h^{2}}=\frac{1}{ b^ {2}}+ frac{1}{c^{2}} .\)

giaibaitap.me