Trong bài viết tiếp theo, chúng tôi sẽ hệ thống lại những kiến thức cơ bản về Lý thuyết tập cố định về hàm số mũ, hàm số mũ, hàm số logarit lớp 12. Hi vọng sẽ hữu ích với mọi người .Cách xác định nhanh và chính xác tập xác định của hàm số mũ, hàm số mũ và hàm số logarit
Tập hợp các hàm mũ xác định
Hàm số mũ y=ax(a > 0; a ≠ 1) không có điều kiện. Tức là tập xác định của nó là r.
Vậy khi bài toán yêu cầu tập cố định y=af(x)(a > 0; a ≠ 1) của hàm số mũ, ta chỉ cần hỏi điều kiện có nghĩa (xác định) của f(x)
Ví dụ 1: Tìm tập hàm
Giải pháp
Điều kiện x2 + 2x- 3 ≥ 0 x 1 hoặc x – 3
Xác định tập hợp là d = ( – ∞; -3] ∪ [1; +∞)
Ví dụ 2: Tìm tập xác định d của hàm số y = (1 – x2)-2018 + 2x – 4
Điều kiện 1 – x2≠0 x≠±1
Xác định tập hợp là d = ( – ∞; -1] ∪ [1; +∞)
Vậy tập xác định của hàm: d = r\ ( -1, 1 )
Ví dụ 3: Tìm tập xác định d của hàm số
Hàm xét đoán khi và chỉ khi
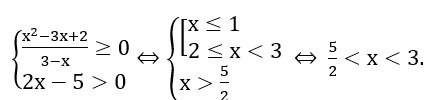
Xem Thêm: Điều Khoản Sử Dụng Hitclub: Hướng Dẫn Chi Tiết Cho Người Chơi
Vậy tập xác định của hàm số là d=(5/2; 3).
Tập hợp các hàm mũ xác định
Hàm lũy thừa là một hàm có dạng y = xα (α ∈ r). Có nhiều bộ định nghĩa khác nhau cho hàm mũ, tùy thuộc vào α:
- Nếu α là số nguyên dương thì tập các định thức là r
- Nếu α là một nguyên âm hoặc α = 0, tập hợp các định thức là r∖{0}
- Nếu α không phải là số nguyên thì tập xác định là (0; +∞).
- Hàm số y = √x có tập xác định là [0; +∞).
- Hàm số y = 3√x có tập xác định r và các hàm số = x½, y = x1/3 có tập xác định (0; +∞).
- Công thức số học bổ sung
- Các công thức gốc cho đạo hàm căn bậc hai, lượng giác, logarit, a – z
- Giải phương trình bậc hai
- Hàm logarit y=logax, (a > 0; a ≠ 1) có tập xác định là d = (0; +∞)
- Hàm logarit y=logaf(x), (a > 0; a ≠ 1) được định nghĩa là
- Hàm số y = logg(x)f(x), (g(x) > 0; g(x) ≠ 1) có điều kiện xác định là
- Hàm số y = (f(x))g(x) xác định ⇔ f(x) > 0
Lưu ý:
Ví dụ 1:
Đã tìm thấy tập hợp các hàm sau:
A. y=x3
y=x½ y=x-√3
y=e√2×2- 8
A. y=x3 Vì 3 là số nguyên dương nên tập xác định của hàm số là: d = r
y=x½ Vì 1/2 là số hữu tỉ, không phải số nguyên nên tập xác định của hàm số là d=\left( 0,+∞ )
y=x-√3 Vì -√3 là số vô tỉ, không phải số nguyên nên tập xác định của hàm số là: d=( 0,+∞ )
Điều kiện xác định của hàm số 2×2-8 ≥ 0
; x ∈ ( – ∞; -4] ∪ [4; +∞)
Vậy tập xác định của hàm: d = r\ ( -4, 4 )
Xem Thêm: Mẫu giấy cam kết không tranh chấp tài sản thừa kế
Ví dụ 2:

; x ∈ ( – ∞; – 1] [4; + ∞)
Ví dụ 3: Tìm tập xác định d của hàm số
Giải pháp
Hàm xét đoán khi và chỉ khi
Vậy tập xác định của hàm số là d = (-4 ; 4)\{-2 ,2}.
Trích dẫn:
Tập xác định của các hàm logarit
Ví dụ 1: Tìm tập xác định của hàm số: y = log3(22x – 1)
Điều kiện phán đoán của hàm: 22x-1 > 0 => x > 0 => d = ( 0,+∞)
Ví dụ 2: Tìm tập xác định của hàm số y=(x2-16)-5-ln(24-5x-x2).
Tập hợp các định nghĩa của hàm số y = (x2-16)-5 – ln(24-5x-x2) là:
Vậy tập hợp là: d=(-8;3)\{-4}.
Ví dụ 3: Tìm điều kiện xác định của hàm số: y = log2( x2-5x+6 )
Xem Thêm: Thông tin giải đáp Add có nghĩa là gì dành cho người chưa biết
Điều kiện xét của hàm số: x2- 5x + 6 > 0
; x ( – ∞; 2) (3; + ∞)
Ví dụ 4: Tìm tập hợp hàm
Khi nào một chức năng có ý nghĩa
⇔ 3x+1 > 0 ⇔ x > -1/3.

Ví dụ 5: Tìm tập hợp tất cả các giá trị của tham số m để hàm số y=log2(4x-2x+m) có tập xác định d=r.
Giải pháp:
Hàm số có tập xác định d = r khi 4x – 2x + m > > 0, (1), x ∈ r
Đặt t = 2x, t > 0
Khi đó (1) trở thành t2 – t + m > 0 ⇔ m > – t2 + t, t ∈ (0;+∞)
Đặt f(t) = -t2 + t
Liệt kê sự biến thiên của hàm số f(t) = -t2 + t trên khoảng (0;+∞)
hỏi khi sự cố xảy ra
Mong rằng những kiến thức mà chúng tôi vừa giới thiệu về hàm số mũ, tập xác định của hàm số mũ và hàm số logarit có thể giúp các bạn vận dụng và giải bài tập nhanh chóng


