Hướng dẫn giải bài tập §2. Tổng và hiệu của hai vectơ Chương 1. Vectơ, SGK Hình Học 10. Nội dung giải bài 1 2 3 4 5 6 7 8 9 10 trang 12 SGK Hình Học 10 bao gồm toàn bộ công thức, lý thuyết, phương pháp giải bài tập và các bài tập hình học khác có trong SGK giúp các em học sinh học tốt bài toán lớp 10.
Lý thuyết
1. tổng của hai vectơ
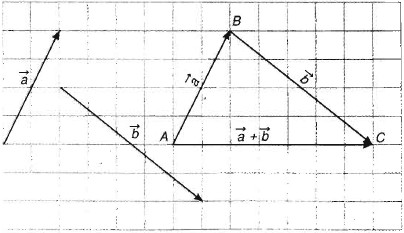
Cho hai vectơ \(\vec a\) và \(\vec b\). Lấy điểm a rồi xác định điểm b, c sao cho \(\vec {ab}=\vec {a}\); \(\vec {bc}=\vec {b} ). Khi đó \(\vec {ac}\) là tổng của hai vectơ \(\vec a\) và \(\vec b\) .
Ta viết: \(\vec {ac}=\vec{a}+\vec{b}\)
2. Các tính chất của phép cộng véc tơ
Tính tương thích: \(\vec{a}+\vec{b}=\vec{b}+\vec{a}\)
Thuộc tính liên kết: \((\vec{a}+\vec{b})+\vec{c}=\vec{a}+(\vec{b}+ vec {c})\)
Thuộc tính số 0 của vectơ: \(\vec{a}+\vec{0}=\vec{a}\)
3. Quy tắc hình bình hành
a) Quy tắc một phần ba
Với ba điểm a, b, c bất kỳ ta luôn có: \(\vec{ab}+\vec{bc}=\vec{ac}\)
b) Quy tắc hình bình hành

Vì abcd là hình bình hành nên ta luôn có: \(\vec{ab}+\vec{ad}=\vec{ac}\)
Ghi chú:
Nếu m là trung điểm của đoạn thẳng ab thì \(\vec{ma}+\vec{mb}=\vec{0}\)
Nếu g là trọng tâm của tam giác abc thì \(\vec{ga}+\vec{gb}+\vec{gc}=\vec{0}\)
4. Vectơ nghịch đảo của một vectơ
Nếu tổng của hai vectơ \(\vec a\) và \(\vec b\) bằng 0 thì vectơ \(\vec a\) được nói là vectơ đối tượng của vectơ \(\vec b\) và ngược lại vectơ \(\vec b\) là vectơ \(\vec a\)
Vectơ nghịch đảo của vectơ \(\vec a\) là vectơ ngược hướng với vectơ \(\vec a\) và có cùng kích thước bằng).
Vectơ đối của số 0 cũng chính nó
5. Hiệu của hai vectơ
Ta có: \(\vec{a}-\vec{b}\) = \(\vec{a}+ (-\vec{b})\)
Dưới đây là đáp án các câu hỏi và bài tập sinh hoạt học sinh lớp 10.
Câu hỏi
1. Trả lời câu 1 trang 9 SGK hình học 10
Kiểm tra tính chất của phép cộng trong Hình 1.8.

Trả lời:

2. Trả lời câu hỏi 2 trang 10 SGK Hình học
Vẽ hình bình hành $abcd$. Nhận xét độ dài và hướng của hai vectơ \(\vec{ab}\) và \(\vec{cd}\).
Trả lời:
Ta vẽ hình bình hành $abcd$ như sau:

Nhận xét:
Về độ dài: hai vectơ \(\vec{ab}\) và \(\vec{cd}\) có cùng độ dài.
Hướng: Hai vectơ \(\vec{ab}\) và \(\vec{cd}\) ngược hướng.
3. Trả lời câu hỏi 3 trang 10 SGK Hình học 10
Cho \(\vec{ab}\) + \(\vec{bc}\) = \(\vec{0}\). chỉ ra rằng \(\vec{bc}\) là vectơ nghịch đảo của \(\vec{ab}\).
Trả lời:
Ta có:
\(\eqalign{ & \overrightarrow {ab} + \overrightarrow {bc} = \overrightarrow 0 \leftrightarrow \overrightarrow {ab} + \overrightarrow {bc} – \overrightarrow {bc} = \overrightarrow 0 – \overrightarrow {bc} \cr & \leftrightarrow \overrightarrow {ab} = – \overrightarrow {bc} \cr} \)
Vậy vectơ bc là tia đối của vectơ ab
4. Trả lời câu hỏi 4 Trang 11 SGK Hình học 10
Hãy giải thích tại sao hiệu của hai vectơ \(\vec{ob}\) và \(\vec{oa}\) là một vectơ \(\vec{ab}\ )
Trả lời:
Ta có:
Xem Thêm: Sử dụng Service trong Angular
\(\overrightarrow {ob} – \overrightarrow {oa} = \overrightarrow {ob} + \overrightarrow {ao} = \overrightarrow {ao} + \overrightarrow {ob} = \ mũi tên sang phải {ab} \) (dpcm)
Dưới đây là Lời giải bài 1 2 3 4 5 6 7 8 9 10 trang 12 SGK Hình học 10, các em đọc kĩ đề trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn toàn bộ Bài tập Hình học 10 có lời giải chi tiết Bài 1 2 3 4 5 6 7 8 9 10 Trang 12 SGK Hình Học 10 Bài §2. Tổng và hiệu của hai vectơ từ Chương 1. Vector để bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Trả lời 1 Trang 12 SGK Hình học 10
Cho đoạn thẳng ab và điểm m nằm giữa a và b sao cho $am >;M. Vẽ các vectơ $\overrightarrow{ma} +\overrightarrow{mb}$ và $\overrightarrow{ma} -\overrightarrow{mb}$.
Giải pháp thay thế:
Trên đoạn thẳng chấm, lấy điểm c sao cho: $\overrightarrow{ac} =\overrightarrow{mb}$
⇒ $\overrightarrow{ma} +\overrightarrow{mb}=\overrightarrow{ma} +\overrightarrow{ac}$
⇔ $\overrightarrow{ma} +\overrightarrow{mb}=\overrightarrow{mc}$
Tương tự: $\overrightarrow{ma} -\overrightarrow{mb}=\overrightarrow{ma}+(-\overrightarrow{mb})$
⇔ $\overrightarrow{ma} +\overrightarrow{bm}=\overrightarrow{ba}$.
2. Giải bài 2 SGK Hình học 10 trang 12
Cho hình bình hành $abcd$ và điểm bất kỳ $m$. Chứng minh: $\overrightarrow{ma} +\overrightarrow{mc}=\overrightarrow{mb}+\overrightarrow{md}$
Giải pháp thay thế:

Vì $abcd$ là hình bình hành ⇒ $\overrightarrow{ba} = -\overrightarrow{dc}$
⇒ $\overrightarrow{ba} +\overrightarrow{dc}=\overrightarrow{0}$
Mặt khác: $\overrightarrow{ma} + \overrightarrow{mc} = (\overrightarrow{mb} + \overrightarrow{ba}) + (\overrightarrow{md} + \overrightarrow{dc } )$
⇔ $\overrightarrow{ma} + \overrightarrow{mc} = \overrightarrow{mb} + \overrightarrow{md} + \overrightarrow{ba} + \overrightarrow{dc}$
⇔ $\overrightarrow{ma} + \overrightarrow{mc} = \overrightarrow{mb} + \overrightarrow{md}$ (dpcm)
3. Giải bài 3 Trang 12 SGK Hình học 10
Chứng minh rằng với mọi tứ giác $abcd$ ta luôn có:
a) $\overrightarrow{ab} +\overrightarrow{bc}+\overrightarrow{cd}+\overrightarrow{da}=\overrightarrow{0}$
b) $\overrightarrow{ab} -\overrightarrow{ad}=\overrightarrow{cb}+\overrightarrow{cd}$
Giải pháp thay thế:
Ta có:
a) $\overrightarrow{ab} + \overrightarrow{bc} + \overrightarrow{cd} + \overrightarrow{da}$
= $(\overrightarrow{ab} + \overrightarrow{bc})+(\overrightarrow{cd} + \overrightarrow{da})$
= $\overrightarrow{ac} + \overrightarrow{ca} = \overrightarrow{aa} = \overrightarrow{0}$ (dpcm)
b) $\overrightarrow{ab} – \overrightarrow{ad} = \overrightarrow{ab} + \overrightarrow{da} = \overrightarrow{db}$
$\overrightarrow{cb} + \overrightarrow{cd} = \overrightarrow{db}$
⇒ $\overrightarrow{ab} – \overrightarrow{ad} = \overrightarrow{cb} + \overrightarrow{cd}$ (dpcm)
4. Giải bài 4 Trang 12 SGK Hình học 10
Tam giác $abc$. Vẽ hình bình hành bên ngoài tam giác: $abij, bcpq, cars.$
Bằng chứng: $\overrightarrow{rj} + \overrightarrow{iq} + \overrightarrow{ps} = \overrightarrow{0}$
Giải pháp thay thế:

Ta có: $\overrightarrow{aj} = \overrightarrow{bi} = -\overrightarrow{ib}$
$\overrightarrow{cs} = -\overrightarrow{ra}$
$\overrightarrow{pc} = -\overrightarrow{bq}$
⇒ $\overrightarrow{rj} + \overrightarrow{iq} + \overrightarrow{ps}$
= $(\overrightarrow{ra} + \overrightarrow{aj}) + (\overrightarrow{ib} + \overrightarrow{bq})(\overrightarrow{pc} + \overrightarrow{cs} )$
Xem Thêm: Hóa 12 | Giải bài tập SGK Hóa học 12 hay nhất, chi tiết
= $(\overrightarrow{ra} + \overrightarrow{-ib}) + (\overrightarrow{ib} + \overrightarrow{-pc}) + (\overrightarrow{pc} + \overrightarrow {-ra})$
= $(\overrightarrow{ib} + \overrightarrow{-ib}) + (\overrightarrow{pc} + \overrightarrow{-pc}) + (\overrightarrow{ra} + \overrightarrow {-ra}) = \overrightarrow{0}$ (dpcm)
5. Giải bài 5 Trang 12 SGK Hình Học 10
Tam giác đều $abc$ có các cạnh bằng $a$. Tính độ dài của các vectơ $\overrightarrow{ab} +\overrightarrow{bc}$ và $\overrightarrow{ab} -\overrightarrow{bc}$.
Giải pháp thay thế:

Ta có: $\overrightarrow{ab} +\overrightarrow{bc}=\overrightarrow{ac}$
⇒ $\left |\overrightarrow{ab} +\overrightarrow{bc} \right |=ac=a$
man $\overrightarrow{ad} =\overrightarrow{bc}$
⇒ $\overrightarrow{ab} -\overrightarrow{bc}=\overrightarrow{ab} -\overrightarrow{ad}=\overrightarrow{db}$
Coi $i$ là giao điểm của $ac$ và $bd$.
Trong đó $abcd$ là hình thoi ⇒ $i$ là hình vuông có trung điểm $bd$ và $i$.
⇒ $bi=ab\sin a = a\sin 60^{\circ} = \frac{a\sqrt{3}}{2}$
⇒ $bd = 2bi = a\sqrt{3}$
⇒$\left |\overrightarrow{ab} – \overrightarrow{bc} \right | = a\sqrt{3}$.
6. Giải bài 6 Trang 12 SGK Hình học 10
Cho hình bình hành $abcd$ có tâm $o$. Bằng chứng:
a) $\overrightarrow{co}-\overrightarrow{ob}=\overrightarrow{ba}$
b) $\overrightarrow{ab}-\overrightarrow{bc}=\overrightarrow{db}$
c) $\overrightarrow{da}-\overrightarrow{db}=\overrightarrow{oa}-\overrightarrow{ob}$
d) $\overrightarrow{da}-\overrightarrow{db}+\overrightarrow{dc}=\overrightarrow{0}$
Giải pháp thay thế:
Áp dụng quy tắc hình bình hành, ta có:
a) $\overrightarrow{co} – \overrightarrow{ob}$ = $\overrightarrow{co}+\overrightarrow{od}$
= $\overrightarrow{cd}=\overrightarrow{ba}$ (dpcm)
b) $\overrightarrow{ab}-\overrightarrow{bc}$ = $\overrightarrow{ab}+(-\overrightarrow{bc})$
= $\overrightarrow{ab}+\overrightarrow{da}$ = $\overrightarrow{db}$ (dpcm)
c) Ta có: $\overrightarrow{da}-\overrightarrow{db}=\overrightarrow{ba}$
$\overrightarrow{oa}-\overrightarrow{ob}=\overrightarrow{od}-\overrightarrow{oc}=\overrightarrow{cd}$
$\overrightarrow{ba}=\overrightarrow{cd}$
⇒ $\overrightarrow{da}-\overrightarrow{db}=\overrightarrow{oa}-\overrightarrow{ob}$ (dpcm)
d) $\overrightarrow{da}-\overrightarrow{db}+\overrightarrow{dc}$
= $\overrightarrow{ba}+\overrightarrow{dc}$ = $\overrightarrow{ba}+\overrightarrow{ab}=\overrightarrow{0}$ (dpcm)
7.Giải bài tập trang 7 SGK hình học 12
Cho vectơ $a, b$ là hai vectơ $0 khác nhau. Khi bình đẳng tồn tại:
a) $\left| \overrightarrow{a} +\overrightarrow{b}\right |=\left | \overrightarrow{a} \right|+\left| \overrightarrow {b}\right|$
b) $\left| \overrightarrow{a} +\overrightarrow{b}\right |=\left | \overrightarrow{a}-\overrightarrow{b} \right |$
Giải pháp thay thế:
a) Hãy xem xét: \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} right |\) + \(\left | \overrightarrow{b} \right |\)
Giả sử hình bình hành \(abcd\) có kích thước \(\overrightarrow {ab} = \overrightarrow {dc} = \overrightarrow a ,\;\;\overrightarrow {ad} = overrightarrow {bc} = \overrightarrow b .\)
Khi đó ta có: \(\overrightarrow a + \overrightarrow b = \overrightarrow {ab} + \overrightarrow {bc} = \overrightarrow {ac} \)\( \rightarrow left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow {ac} } \right| = ac.\)
Một lần nữa: \(\left| {\overrightarrow a } \right| + \left| {\overrightarrow b } \right| = a + b = ab + bc.\)
Xem Thêm: Dán Skin Máy Ảnh Chuyên Nghiệp | Thiết Kế Skin Trang Trí Máy Ảnh Theo Yêu Cầu
\( \rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a } \right| + \left| { overrightarrow b } \right|\)\( \leftrightarrow ac = ab + bc\)
\( \leftrightarrow a, \, \, b,\, \, c\) trong \(a, \, , c\) hoặc \( overrightarrow a ,\;\overrightarrow b \) cùng hướng.
Vì vậy \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |+ \left | \ overrightarrow{b} \right |\) khi hai vectơ \(\overrightarrow{a}, \, \, \overrightarrow{b}\) cùng hướng.
b) Xem xét \(\left | \overrightarrow{a}+\overrightarrow{b} \right |= \left | \overrightarrow{a}- overrightarrow{b} \right|.\)
Tương tự a) ta có: \( \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow {ac} } \right| = Giao tiếp\)
Ta có: \(\overrightarrow a – \overrightarrow b = \overrightarrow {ab} – \overrightarrow {ad} = \overrightarrow {db} \) \( \rightarrow \ Trái | {\overrightarrow a – \overrightarrow b } \right| = \left| {\overrightarrow {db} } \right| = db.\)
\( \rightarrow \left| {\overrightarrow a + \overrightarrow b } \right| = \left| {\overrightarrow a – \overrightarrow b } \right| \ )\(\leftrightarrow ac = db.\)
Khi đó hình bình hành \(abcd\) là hình chữ nhật \(\rightarrow ad \perp ab\) hoặc \(\overrightarrow{a}\perp\overrightarrow{ b}. )
8.Giải bài tập Trang 8 12 SGK Hình học 10
Đối với $\left | \overrightarrow{a} +\overrightarrow{b}\right |= \overrightarrow{0}$.
So sánh độ dài, phương và hướng của hai vectơ $a$ và $b$.
Giải pháp thay thế:
Theo bài viết: $\left | \overrightarrow{a} +\overrightarrow{b}\right |= \overrightarrow{0}$
⇒ $\overrightarrow{a} = -\overrightarrow{b}$
⇒ Hai vectơ cùng phương, cùng độ lớn và ngược hướng.
9.Giải bài tập Trang 9 12 SGK Hình học 10
Bằng chứng: $\overrightarrow{ab} =\overrightarrow{cd}$ khi và chỉ khi trung điểm của hai đoạn thẳng $ad$ và $bc$ trùng nhau.
Giải pháp thay thế:
Nếu $\overrightarrow{ab} =\overrightarrow{cd}$
⇒ $ab // cd, ab = cd$
⇒ $abcd$ là hình bình hành.
Vậy thì $ad$ và $bc$ có cùng trung điểm.
Ngược lại: nếu trung điểm của $ad$ và $bc$ trùng nhau
⇒ tứ giác $abcd$ là hình bình hành.
⇒ $\overrightarrow{ab} =\overrightarrow{cd}$ (dpcm )
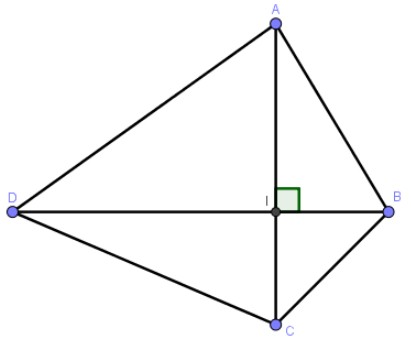
10. Giải bài 10 trang 12 SGK Hình học
Ba lực $\overrightarrow{f_{1}} =\overrightarrow{ma}$ ; $\overrightarrow{f_{2}} =\overrightarrow{mb}$ , $\overrightarrow{f_ { 3}} =\overrightarrow{bc}$ có tác dụng tương tự
Tại điểm $m$ đối với một đối tượng, đối tượng đó đang đứng yên. Cho biết độ lớn của hai lực $f_{1}, f_{2}$ đều là 100n, $\widehat{amb}=60^{\circ}$.
Tìm độ lớn và hướng của lực $f_{3}$.
Giải pháp thay thế:

Theo bài báo: $ma = mb = 100n$
$\widehat{amb} = 60^{\circ}$
⇒ $\triangle amb$ là tam giác đều.
⇒ $mh = \frac{ma\sqrt{3}}{2} = 50\sqrt{3}(n)$
Vì $ambc$ là hình thoi ⇒ $mc = 2mh$.
⇒ $mc = 100\sqrt{3}(n)=f_{3}$
Vậy $f_{3}=100\sqrt{3}(n)$ và hướng của nó là tia phân giác của $\widehat{amb}$.
Trước:
- Giải 1 2 3 4 Trang 7 SGK Hình Học 10
- Giải 1 2 3 4 5 6 7 8 9 Trang 17 SGK Hình Học 10
- Câu hỏi khác 10
- Học tốt vật lý lớp 10
- Học tốt môn sinh học lớp 10
- Học tốt ngữ văn lớp 10
- Điểm tốt môn lịch sử lớp 10
- Học tốt môn địa lý lớp 10
- Học tốt tiếng Anh lớp 10
- Học tiếng Anh lớp 10 thí điểm
- Học tốt tin học lớp 10
- Học chăm chỉ vào lớp 10 gdcd
Tiếp theo:
Xem thêm:
Chúc các bạn làm tốt bài tập giải bài tập SGK toán 10 tập 1 2 3 4 5 6 7 8 9 10 trang 12 SGK hình học 10!
“Môn thể thao nào đã khó giabaisgk.com”


