Vận dụng các kiến thức liên quan về lăng kính, phản xạ, khúc xạ, phản xạ toàn phần trong Vật lý 11 để thực hành hiện tượng tán sắc ánh sáng.
Lý thuyết và thực hành tán sắc ánh sáng (Hoàn thành)
I. Lý thuyết
* Tán sắc quang học: Tán sắc quang học là sự phân tách một chùm ánh sáng phức hợp thành các chùm sáng đơn sắc.
* Ánh sáng đơn sắc, ánh sáng trắng
– Ánh sáng đơn sắc là ánh sáng không bị tán sắc khi đi qua lăng kính. Mỗi ánh sáng đơn sắc có một màu gọi là ánh sáng đơn sắc. Mỗi màu trong mọi môi trường đều có một bước sóng nhất định.
– Khi truyền qua các môi trường trong suốt khác nhau thì vận tốc ánh sáng thay đổi, bước sóng ánh sáng thay đổi nhưng tần số ánh sáng không thay đổi.
– Ánh sáng trắng là tập hợp của vô số ánh sáng đơn sắc khác nhau, có màu khác nhau từ đỏ đến tím.
– Dải cầu vồng (có vô số màu nhưng chia thành 7 màu chính đỏ, da cam, vàng, lục, lam, chàm, tím) gọi là quang phổ của ánh sáng trắng.
– Chiết suất của các chất trong suốt thay đổi theo màu của ánh sáng, tăng dần từ đỏ đến tím.
* Ứng dụng tán sắc ánh sáng
– Máy quang phổ phân tách ánh sáng đa sắc từ một vật sáng thành ánh sáng đơn sắc.
– Hiện tượng cầu vồng là do hiện tượng tán sắc ánh sáng, khúc xạ và phản xạ ánh sáng mặt trời của các giọt nước trước khi đến mắt chúng ta
Giải pháp thay thế:
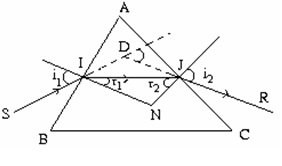
Áp dụng công thức Lăng trụ:
+Công thức tổng quát: sini1 = n sinr1
sini2 = n sinr2
a = r1 + r2
d = i1 + i2 – a
+trường hợp i và a đều bé: i1 = nr1; i2 = nr2; d = (n – 1)a
+Độ từ thiên tối thiểu:
+Công thức độ lệch tối thiểu: \(sin\frac{d_{min}+a}{2}=nsin\frac{a}{2}\) p>
¨ Điều kiện để có phản xạ toàn phần: n1 > n2; i> và sinigh = \(\frac{n_{2}}{n_{1}}\)
¨ Với ánh sáng trắng: \(\left\{\begin{matrix} n_{heart}\geq n_{\lambda }\geq n_{do} & & \ \lambda _{tim}\leq \lambda \leq \lambda _{do} & & \end{matrix}\right.\)
Hai. Loại bài tập
Một. Kiến thức:
Tán sắc ánh sáng là hiện tượng chùm sáng phức tạp bị phân cắt thành chùm sáng đơn sắc.
Lý do của hiện tượng tán sắc là do chiết suất của môi trường thay đổi theo màu của ánh sáng, tăng dần từ đỏ sang tím: (nred < ncam < nvàng < nxanh < nlam < chàm < nt tím.)
=>Độ lệch Tia đỏ thấp nhất, Tia tímĐộ dịch chuyển Hầu hết .
Bước sóng ánh sáng trong chân không: \(\lambda =\frac{c}{f}\) ; c = 3,108 m/s.
Bước sóng của ánh sáng trong môi trường: \(\lambda ‘=\frac{v}{f}=\frac{c}{nf}=\frac{\lambda}{n} ).
Khi truyền từ môi trường trong suốt này sang môi trường trong suốt khác thì vận tốc ánh sáng thay đổi, bước sóng ánh sáng thay đổi nhưng tần số (chu kì, tần số góc) của ánh sáng không đổi. .
Thông thường các câu hỏi liên quan đến công thức lăng kính:
+Công thức chung: sini1 = nsinr1; sini2 = nsinr2; a = r1 + r2; d = i2 + i2 – a.
d = dmin và sin = n (đối xứng) khi i1 = i2 (r1 = r2)
+ Khi góc khúc xạ a và góc tới i1 đều nhỏ (≤100) ta có công thức gần đúng:
i1 = nr1; i2 = nr2; one = r1 + r2; d = a(n – 1); dmin = a(n – 1).
+ Khi cần thiết, một số câu hỏi liên quan đến định luật phản xạ:
i = i’, định luật khúc xạ: n1sini1 = n2sini2.
b.Thực hành:
Bản phát hành 1. Bước sóng của ánh sáng đỏ trong không khí là 0,64 μm. Biết chiết suất của nước đối với ánh sáng đỏ là \(\frac{4}{3}\), hãy tính bước sóng của ánh sáng trong nước.
Giải phápĐiều1. Ta có: \(\lambda’=\frac{v}{f}=\frac{c}{nf}=\frac{\lambda}{n}=0,48\mu m )
Phát hành2. Ánh sáng đơn sắc có bước sóng 0,6 μm trong không khí và 0,4 μm trong chất lỏng trong suốt. Tính chiết suất của chất lỏng đối với ánh sáng này.
Giải phápĐiều2. Chúng ta có: \(\lambda ‘=\frac{\lambda }{n}\rightarrow n=\frac{\lambda }{\lambda ‘}=1.5\)
Bản phát hành 3. Một chùm sáng đơn sắc hẹp có bước sóng λ = 0,60 μm trong chân không. Xác định chu kì và tần số của ánh sáng. Tính tốc độ và bước sóng ánh sáng truyền qua thủy tinh có chiết suất n = 1,5.
Giải phápĐiều3. Chúng tôi có:
f = \(\frac{c}{f}\)= 5.1014 Hz; t = \(\frac{1}{f}\)= 2.10-15 giây; v = (\frac{c}{n}\) = 2.108 m/s; λ’ = \(\frac{v}{f}=\frac{\lambda}{n}\) = 0,4 μm.
Phát hành4. Lăng kính có góc chiết quang 600 . Biết chiết suất của lăng kính đối với ánh sáng đỏ là 1,5. Dùng mặt bên của lăng kính có góc tới 600 để chiếu ánh sáng đỏ, tính góc lệch giữa tia sáng đi và tia tới.
Giải phápĐiều4. Chúng tôi có:
sinr1 = \(\frac{sini_{1}}{n}\) = 0,58 = sin35,30 => r1 = 35,30 => r2 = a – r1 = 24,70;
sini2 = nsinr2 = 0,63 = sin38,00 => i2 = 38,80 => d = i2 + i2 – a = 38,80.
Phát hành5. Một lăng kính thủy tinh có góc chiết quang a = 600 có chiết suất đối với tia đỏ là 1,514, đối với tia tím là 1,532. Tính góc lệch cực tiểu của hai tia này.
Giải phápĐiều5. Tia đỏ: sin\(\frac{d_{dmin}+a}{2}\) = ndsin\(\frac{a}{2}\)= sin49,20 => ( \frac{d_{dmin}+a}{2}\) = 49,20 =>dmin = 2,49,20 – a = 38,40 = 38024′. Màu tím: sin \(\frac{d_{dmin}+a}{2}\) = ntsin\(\frac{a}{2}\)= sin500 =>\( frac {d_{dmin}+a}{2}\)= 500 =>dtmin = 2.500 – a = 400.
Phát hành6. Một lăng kính thủy tinh có góc khúc xạ a = 40 đặt trong không khí. Các lăng kính có chiết suất lần lượt là 1,643 và 1,685 đối với ánh sáng đỏ và tím. Chiếu một chùm tia hẹp đỏ tím vào mặt bên của lăng kính theo phương vuông góc với mặt lăng kính. Tính góc hợp bởi tia đỏ và tia tím khi ló ra khỏi mặt bên kia của lăng kính.
Giải phápĐiều6. Với a và i1 nhỏ (£100), ta có: d = (n – 1)a.
Do đó: dd = (nd = 1)a; dt = (nt – 1)a.
Góc tạo bởi tia lửa đỏ và tia lửa tím là: Δd = dt – dd = (nt – nd)a = 0,1680 ≈ 10′.
Phát hành7. Một chùm ánh sáng vàng đơn sắc từ không khí (giả sử mọi ánh sáng đều có chiết suất bằng 1) chiếu tới mặt phân cách của một chất rắn trong suốt với góc tới 600 và ánh sáng bị phản xạ trở lại một hình vuông trong không khí. Góc mà tia khúc xạ đi vào chất rắn. Tính chiết suất của chất rắn trong suốt này đối với ánh sáng vàng.
Giải phápĐiều7. Chúng tôi có:
sini = nsinr = nsin(900 – i’) = nsin(900 – i) = ncosi ð n = tani = \(\sqrt{3}\).
Phát hành8. Một tia sáng gồm các thành phần đỏ và tím của không khí (giả sử mọi ánh sáng đều có chiết suất bằng 1) chiếu với một góc tới 600 trên mặt phẳng của khối thủy tinh. Biết rằng chiết suất của thủy tinh đối với ánh sáng đỏ là 1,51; tím là 1,56. Tính góc lệch của hai tia khúc xạ trong thủy tinh.
Giải phápĐiều8. Chúng tôi có:
sinrd = \(\frac{sini}{n_{d}}\) = 0,574 = sin350; sinrt = \(\frac{sini}{n_{t}}\) = 0,555 = sin33,70 => Δr = rd – rt = 1,30.
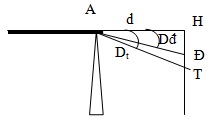
Điều9. (Tháng 12 năm 2011): Một lăng kính có góc khúc xạ a = 60 (được coi là góc nhỏ) được đặt trong không khí. Một chùm ánh sáng trắng song song hẹp được chiếu vào một mặt bên của lăng kính theo phương vuông góc với tia phân giác của góc khúc xạ, rất sát mép của lăng kính. Đặt một màn e phía sau lăng kính, vuông góc với phương truyền của chùm tia tới, cách tia phân giác của góc khúc xạ một đoạn 1,2 m. Chiết suất của lăng kính ánh sáng đỏ là nd = 1,642 và của lăng kính ánh sáng tím là nt = 1,685. Bề rộng của quang phổ liên tục quan sát được trên màn từ màu đỏ đến màu tím là
a. 5,4 mm. b. 36,9 mm. c. 4,5 mm. d. 10,1 mm.
Giải: Sử dụng công thức để tính gần đúng độ nghiêng của lăng kính: d = (n-1)a
Ta có: dt = (1,685-1)6; dd = (1,642-1)6
Nhập máy tính và lưu ý đơn vị của góc là độ (fx570es chọn chế độ shitf 3)
Độ rộng phổ: l= d (tagdt – tagdđ ) = 1200(tan(0.685×6) -tan(0.642×6) )
l= d (tagdt – tagdđ )= 5.429719457 (mm) = 5.4mm.
Chọn một
Tất cả nội dung bài viết. Vui lòng xem thêm và tải về các tài liệu chi tiết sau:
Tải xuống
Bài tập trắc nghiệm Vật Lý lớp 12 – Xem ngay
