Có thể bạn đã quen thuộc với hằng phương trình đáng nhớ. Hôm nay chúng ta sẽ thảo luận chi tiết về 7 hằng đẳng thức quan trọng: tổng bình phương, hiệu bình phương, hiệu hai bình phương, tổng lập phương, hiệu lập phương, tổng hai lập phương và cuối cùng là hiệu hai lập phương. Vui lòng tham khảo trước.
A. 7 hằng đẳng thức đáng nhớ
1. Bình phương của tổng
a, b là các biểu thức tùy ý, ta có: ( a + b )2 = a2 + 2ab + b2.
Ví dụ:
a) Tính ( a + 3 )2. b) Viết biểu thức x2+ 4x + 4 dưới dạng bình phương của tổng.
Hướng dẫn:
a) Ta có: ( a + 3 )2= a2+ 2.a.3 + 32 = a2 + 6a + 9. b) Ta có x2+ 4x + 4 = x2+ 2.x.2 + 22 = ( x + 2 )2.
2. Chênh lệch bình phương
a, b là các biểu thức tùy ý, ta có: ( a – b )2 = a2 – 2ab + b2.
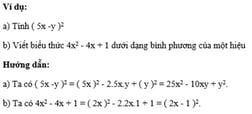
3. Sự khác biệt giữa hai hình vuông
a, b là các biểu thức tùy ý, ta có: a2 – b2 = ( a – b )( a + b ).
4. Lập phương của tổng
a, b là các biểu thức tùy ý, ta có: ( a + b )3 = a3 + 3a2b + 3ab2 + b3.
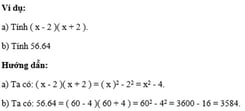
5. Khối khác biệt.
a, b là các biểu thức tùy ý, ta có: ( a – b )3 = a3 – 3a2b + 3ab2 – b3.
Ví dụ:
a) Tính ( 2x – 1 )3. b) Viết biểu thức x3- 3x2y + 3xy2- y3 dưới dạng lập phương sai.
Hướng dẫn:
a) Ta có: ( 2x – 1 )3
= ( 2x )3 – 3.( 2x )2.1 + 3( 2x ).12 – 13
= 8×3 – 12×2 + 6x – 1
b) Ta có: x3- 3x2y + 3xy2- y3
= ( x )3 – 3.x2.y + 3.x. y2 – y3
= ( x – y )3
6. Tổng của hai lập phương
a, b là các biểu thức tùy ý, ta có: a3 + b3 = ( a + b )( a2 – ab + b2 ).
Lưu ý: Ta đồng ý rằng a2 – ab + b2 là bình phương còn thiếu của hiệu a – b.
Ví dụ:
a) Tính 33+ 43. b) Viết biểu thức ( x + 1 )( x2- x + 1 ) dưới dạng tổng hai lập phương.
Hướng dẫn:
a) Ta có: 33+ 43= ( 3 + 4 )( 32 – 3.4 + 42 ) = 7.13 = 91. b) Ta có: ( x + 1 )( x2- x + 1 ) = x3+ 13 = x3 + 1.
7. Sự khác nhau giữa hai hình lập phương
a, b là các biểu thức tùy ý, ta có: a3 – b3 = ( a – b )( a2 + ab + b2 ).
Lưu ý: Chúng ta đồng ý rằng a2 + ab + b2 là bình phương còn thiếu của tổng a + b.
Ví dụ:
a) Tính 63- 43. b) Viết biểu thức ( x – 2y )( x2+ 2xy + 4y2) dưới dạng hiệu của hai lập phương
Hướng dẫn:
a) Ta có: 63- 43= ( 6 – 4 )( 62 + 6.4 + 42 ) = 2.76 = 152. b) Ta có: ( x – 2y )( x2+ 2xy + 4y2) = ( x )3 – ( 2y )3 = x3 – 8y3.
b. Bài tập tự luyện về đẳng thức
Bài 1. tìm x biết
a) ( x – 3 )( x2+ 3x + 9 ) + x( x + 2 )( 2 – x ) = 0. b) ( x + 1 )3- ( x – 1 )3- 6( x – 1 )2 = – 10.
Hướng dẫn:
a) Áp dụng hằng đẳng thức ( a – b )( a2+ ab + b2) = a3 – b3.
( a – b )( a + b ) = a2 – b2.
Khi đó ta có ( x – 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.
⇔ x3 – 33 + x( 22 – x2 ) = 0 ⇔ x3 – 27 + x( 4 – x2 ) = 0
⇔ x3 – x3 + 4x – 27 = 0
⇔ 4x – 27 = 0
Vậy x= 
.
b) Áp dụng hằng đẳng thức ( a – b )3= a3- 3a2b + 3ab2 – b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a – b )2 = a2 – 2ab + b2
Khi đó ta có: ( x + 1 )3 – ( x – 1 )3 – 6( x – 1 )2 = -10.
⇔ ( x3 + 3×2 + 3x + 1 ) – ( x3 – 3×2 + 3x – 1 ) – 6( x2 – 2x + 1 ) = – 10
⇔ 6×2 + 2 – 6×2 + 12x – 6 = – 10
⇔ 12x = -6
Vậy x= 
Bài tập 2: Rút gọn biểu thức a = (x + 2y ).(x – 2y) – (x – 2y)2
- 2×2+ 4xy b. – 8y2+ 4xy
- – 8y2d. – 6y2+ 2xy
- Hãy ghi nhớ
Hướng dẫn
Ta có: a = (x + 2y). (x – 2y) – (x – 2y)2
a = x2 – (2y)2 – [x2 – 2.x.2y +(2y)2 ]
a = x2 – 4y2 – x2 + 4xy – 4y22
a = -8y2 + 4xy
Các hằng phương trình đáng nhớ ở trên rất quan trọng đối với Tủ kiến thức của chúng tôi. Vì vậy, hãy học nó và ghi nhớ nó. Các phương trình này giúp chúng ta giải các bài toán dễ và khó một cách dễ dàng, các bạn nên làm đi làm lại để vận dụng tốt hơn. Chúc các bạn thành công và chăm chỉ học tập. Xem bài viết tiếp theo
