Bài tập §7. Hình bình hành, Chương 1 – Hình tứ giác, SGK Toán 8 Tập 1. Nội dung Giải bài 46 47 48 49 trang 92 93 SGK Toán 8 tập 1 bao gồm tổng hợp các công thức, lý thuyết, phương pháp giải bài tập hình học trong SGK Toán 8, giúp học sinh học tốt môn Toán lớp 8.
Lý thuyết
1. định nghĩa
Hình bình hành là tứ giác có các cạnh đối song song.
abcd là hình bình hành \( \leftrightarrow \) ab // cd và ad // bc.
Hình bình hành là hình thang có hai cạnh đối song song.
2. thuộc tính
Lý thuyết:
Hình bình hành:
a) Các cạnh đối diện thì bằng nhau.
b) Các góc đối đỉnh thì bằng nhau.
c) Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
3. Dấu hiệu nhận biết
- Tứ giác có các cạnh đối song song là hình bình hành.
- Tứ giác có các cạnh đối diện bằng nhau là hình bình hành.
- Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
- Tứ giác có các góc đối bằng nhau là hình bình hành
- Tứ giác có hai đường chéo cắt nhau tại trung điểm là hình bình hành.
- Đáp án bài 43 44 45 trang 92 SGK Toán 8 1
- Giải bài 50 51 52 53 trang 95 96 SGK Toán 8 Tập 1
- Câu hỏi khác 8
- Học tốt vật lý lớp 8
- Học tốt môn sinh học lớp 8
- Học tốt ngữ văn lớp 8
- Điểm tốt môn lịch sử lớp 8
- Học tốt môn địa lý lớp 8
- Học tốt tiếng Anh lớp 8
- Học tốt môn tiếng Anh lớp 8 thí điểm
- Học Khoa học Máy tính Lớp 8
- Học chăm chỉ môn gdcd lớp 8
Dưới đây là hướng dẫn giải bài 1 SGK Toán 8 trang 46 47 48 49 trang 92 93, các em đọc kĩ phần đầu bài trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn toàn bộ phương pháp Giải bài tập phần Hình học 8 với các bài giải chi tiết trang 46 47 48 49 trang 92 93 SGK Toán Tập 1 Bài 7. Hình bình hành trong chương đầu tiên – hình tứ giác dành cho các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 46 trang 92 sgk toán 8 tập 1
Câu sau đây đúng hay sai?
a) Hình thang có hai đáy bằng nhau là hình bình hành.
b) Hình thang có hai cạnh đối song song là hình bình hành.
c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành
d) Hình thang có hai cạnh bên bằng nhau là hình bình hành.
Giải pháp:
b) Đúng, vì khi đó ta được một tứ giác có các cạnh đối song song, là hình bình hành (định nghĩa).
c) Sai, vì hình thang cân có hai cạnh đối diện bằng nhau (hai cạnh bên) nhưng không phải là hình bình hành.
d) Sai vì hình thang cân có hai cạnh bên bằng nhau nhưng không phải là hình bình hành.
2. Giải bài 47 tr.93 SGK Toán 8 1
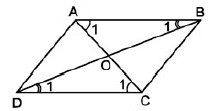
Đối với Hình 72, trong đó $abcd$ là hình bình hành
a) Chứng minh rằng $ahck$ là hình bình hành.
b) Gọi $o$ là trung điểm của $hk$. Chứng minh ba điểm $a, o, c$ thẳng hàng.
Giải pháp:
a) Xét hai tam giác vuông \(ahd\) và \(ckb\):
\( ad = cb\) (vì \(abcd\) là hình bình hành)
\(\widehat {adh} = \widehat {cbk}\) (vị trí so le hai góc)
Suy ra \(Δahd = Δckb\) (cạnh huyền – góc nhọn)
Suy ra \(ah = ck\)
\(ah\bot bd\) và \(ck\bot bd\) suy ra \(ah//ck\)
Tứ giác \(ahck\) có \(ah//ck\) và \(ah = ck\) nên là hình bình hành (theo kí hiệu nhận biết hình bình hành),
p>
b)Ta có đồ thị sau:
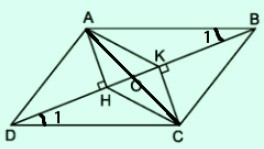
Xét hình bình hành \(ahck\), trong đó \(o\) là trung điểm của \(hk\), nên \(o\) là giao điểm của hai đường chéo \( ac\) và \(hk\) của hình bình hành.
Căn chỉnh
hoặc \(a,o,c\).
3. Giải bài 48 Trang 93 SGK Toán 8 Tập 1
Một tứ giác $abcd$, trong đó $e, f, g, h$ lần lượt là trung điểm của các cạnh $ab, bc, cd, da$. Tứ giác $efgh$ là gì? Tại sao?
Giải pháp:
Tứ giác $efgh$ là hình bình hành.
Bằng chứng:
♦ Phương pháp 1:
$eb = ea, fb = fc$ (gt) nên $ef$ là đường trung bình động của $Δabc.$
Do đó $ef //ac$
Tương tự, $hg$ là đường trung bình động của $Δacd$.
Do đó $hg //ac$
Suy ra $ef // hg (1)$
tương tự như $eh // fg (2)$
Từ (1) và (2) suy ra $efgh$ là hình bình hành (chữ ký 1).
♦ Cách 2:
$ef$ là đường trung bình động của $Δabc$, vì vậy $ef = \frac{1}{2}ac.$
$hg$ là đường trung bình động của $Δacd$, vì vậy $hg = \frac{1}{2}ac.$
Suy ra $ef = hg$
Với $ef // hg$ (đã chứng minh ở trên)
Vậy $efgh$ là hình bình hành (chữ ký 3).
4. Giải bài 49 tr.93 SGK Toán 8 1
Cho hình bình hành $abcd$, gọi $i, k$ lần lượt là trung điểm của $cd, ab$. Đường chéo $bd$ cắt $ai, ck$ theo thứ tự $m$ và $n$. Bằng chứng:
a) $ai // ck$
b) $dm = mn = nb$
Giải pháp:
a) Tứ giác $abcd$ có $ab = cd, ad = bc$ nên là hình bình hành.
Tứ giác $aick$ có $ak // ic, ak = ic$ nên $aick$ là hình bình hành.
Do đó $ai // ck$
b) $Δdcn$ có $di = ic, im // cn.$
(vì $ai // ck$) nên suy ra $dm = mn (1)$
$Δabm$ có $ak = kb$ và $kn // am$ (vì $ai // ck$) nên $mn = nb. (2)$
Từ (1) và (2) suy ra $dm = mn = nb$
Trước:
Tiếp theo:
Xem thêm:
Chúc các bạn tham khảo và giải vở bài tập 46 47 48 49 trang 92 93 SGK toán 8 tập 1 SGK toán 8 thành công!
“Môn thể thao nào đã khó giabaisgk.com”
