Bài 37 Trang 123 – SGK Toán 7 Tập 1
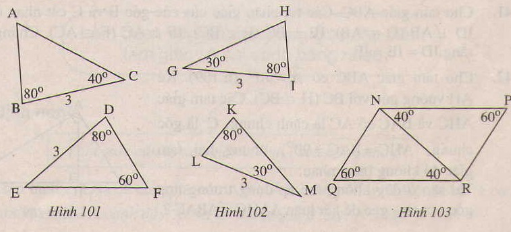
Trong mỗi hình 101,102,103, các tam giác nào bằng nhau? Tại sao?
Người chiến thắng:
Tính các góc còn lại trong mỗi hình vẽ trên, ta được:
Áp dụng định lý tổng tam giác ta có:
\(\eqalign{ & \widehat a = {180^0} – \widehat b – \widehat c = {180^0} – {80^0} – {40^0} = {60^0} \cr & \widehat h = {180^0} – \widehat g – \widehat i = {180^0} – {30^0} – {80^0} = {70^0} \cr & \widehat e = {180^0} – \widehat d – \widehat f = {180^0} – {80^0} – {60^0} = { 40^0} \cr & \widehat l = {180^0} – \widehat k – \widehat m = {180^0} – {80^0} – {30^0} = {70 ^0} \cr & \widehat {qnr} = {180^0} – \widehat {nrq} – \widehat {rqn} = {180^0} – {40^0} – {60^ 0} = {80^0} \cr & \widehat {nrp} = {180^0} – \widehat {rpn} – \widehat {pnr} = {180^0} – {60^0 } – {40^0} = {80^0} \cr} \)
– Xét \(Δabc\) và \(Δfde\) (Hình 101)
+) \(\widehat{b} = \widehat{d}\)
+)\(bc=de\)
+)\(\widehat{c}=\widehat{e}\)
Suy ra \(Δabc=Δfde\) (g.c.g)
– Xem xét \(Δnqr\) và \(Δrpn\) (Hình 103)
+) \(\widehat{qnr}=\widehat{nrp}\) (\(=80^0\))
+) \(nr\) là cạnh chung.
+) \(\widehat{nrq}=\widehat{rnp}\) (\(40^0\))
Suy ra\(Δnqr=Δrpn\) (g.c.g)
– Xem xét \(\delta hig\) và \(\delta lkm\) (Hình 102)
\(\eqalign{& + )\,\,gi = ml \cr & + )\,\,\widehat g = \widehat m \cr & + )\,\,\widehat i = \widehat k \cr} \)
Ta có: \(\widehat g,\; \widehat i\) kề cạnh \(gi\), và \(\widehat m \) kề với cạnh Liền kề thành \(ml\) nhưng \( \widehat k\) không liền kề với \(ml\) nên \(\delta hig\) không bằng \( delta lkm ).
Sau 38 trang 124 – SGK Toán 7
Trong Hình 104, ta có ab//cd, ac//bd. bằng chứng
ab=cd,ac=bd.
Người chiến thắng.
Vẽ một quảng cáo.
Δadb và dac có:
\(\widehat{a_{1}}\)= \(\widehat{d_{1}}\) (xen kẽ trong ab//cd)
Quảng cáo là một lợi thế chung.
\(\widehat{a_{2}}\)=\(\widehat{d_{2}}\) (so le, ac//bd)
Vậy Δadb=Δdac(g.c.g)
Suy luận: ab=cd, bd=ac
Bài 39 Trang 124 – SGK Toán 7
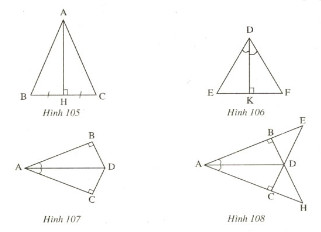
Trong mỗi hình 105,106,108, các tam giác vuông nào bằng nhau? Tại sao?
Người chiến thắng:
Hình 105
\(∆abh\) và \(∆ach\) có:
+) \(bh=ch\) (gt)
+) \(\widehat{ahb}=\widehat{ahc}\) (hình vuông)
+) \(ah\) là cạnh chung.
Vậy \(Δabh=Δach\) (c.g.c)
Hình 106
\(Δdke\) và \(Δdkf\) có:
+) \(\widehat{edk}=\widehat{fdk}\)(gt)
+) \(dk\) là cạnh chung.
+) \(\widehat{dke}=\widehat{dkf}\) (hình vuông)
Vậy \(Δdke=Δdkf\) (g.c.g)
Hình 107
Theo tổng ba góc của tam giác ta có:
\(\eqalign{ & \widehat {abd} + \widehat {bda} + \widehat {dab} = {180^0} \cr & \widehat {acd} + \widehat {cda} + \widehat {dac} = {180^0} \cr} \)
Ngược lại ta có:
\(\eqalign{ & \widehat {dab} = \widehat {dac}\,\,\,(gt) \cr & \widehat {abd} = widehat {acd} = {90^0} \cr} \)
Phải là \(\widehat {bda} = \widehat {cda}\)
Xét \(Δabd\) và \(Δacd\) có:
+) \(\widehat {dab} = \widehat {dac}\,\,\,(gt)\)
+) \(ad\) cạnh chung
+) \(\widehat {bda} = \widehat {cda}\) (cmt)
\(Δabd=Δacd\) (g.c.g)
Hình 108
Theo tổng ba góc của tam giác ta có:
\(\eqalign{& \widehat {abd} + \widehat {bda} + \widehat {dab} = {180^0} \cr & \widehat {acd} + \widehat {cda} + \widehat {dac} = {180^0} \cr} \)
Ngược lại ta có:
\(\eqalign{& \widehat {dab} = \widehat {dac}\,\,\,(gt) \cr & \widehat {abd} = widehat {acd} = {90^0} \cr} \)
Phải là \(\widehat {bda} = \widehat {cda}\)
Xét \(Δabd\) và \(Δacd\) có:
+) \(\widehat {dab} = \widehat {dac}\,\,\,(gt)\)
+) \(ad\) cạnh chung
+) \(\widehat {bda} = \widehat {cda}\) (cmt)
\(Δabd=Δacd\) (g.c.g)
Dẫn xuất: \(bd=cd\) (hai cạnh tương ứng)
\(ab=ac\) (hai cạnh tương ứng)
Xét \(Δdbe\) và \(Δdch\)
+) \( \widehat {ebd} = \widehat {hcd} = {90^0} \)
+)\(bd=cd\) (cmt)
+) \(\widehat {bde} = \widehat {cdh}\) (đối diện)
\(Δdbe=Δdch\) (g.c.g)
Xét \(Δabh\) và \(Δace\)
+) \(\widehat a\) chung
+) \(ab=ac\) (cmt)
+) \(\widehat {abh} = \widehat {ace} = {90^0}\)
\(Δabh=Δace \) (g.c.g)
bài 40 trang 124 – SGK Toán 7
Cho tam giác abc (ab≠ac), tia ax đi qua trung điểm m của bc.
Vẽ be và cf vuông góc với ax (e ∈ ax, f ∈ ax ). So sánh độ dài be và cf/
NGƯỜI CHIẾN THẮNG
Hai tam giác vuông bme và cmf có:
bm=mc(gt)
\(\widehat{bme}\)=\(\widehat{cmf}\) (đối diện)
Vậy bme=Δcmf(góc xiên – góc nhọn).
Suy ra be=cf.
giaibaitap.me
