Bài tập §4. Đường thẳng song song và cắt nhau Chương 2 – Hàm số bậc nhất SGK Toán 9. Nội dung Giải bài 23 24 25 26 trang 55 SGK Toán 9 Tập 1 Các công thức, lý thuyết và phương pháp giải các bài tập đại số trong SGK Toán 9 tổng hợp giúp các em học tốt Toán lớp 9.
Lý thuyết
1. đường thẳng song song
Hai đường thẳng \(y=ax+b(a\neq0)\) và \(y=a’x+b'(a’\neq0)\) song song với nhau , nếu Và chỉ khi \(a=a’\) và \(b\neq b’\) trùng nhau khi và chỉ khi \(a=a’\) và \(b= b ‘ ).
2. đường thẳng cắt nhau
Hai dòng \(y=ax+b(a\neq0)\) và \(y=a’x+b'(a’\neq0)\) tồn tại và chỉ khi (a\neq a’\).
Lưu ý: Khi hai đường thẳng \(a\neq a’\) và \(b=b’\) có cùng gốc tọa độ thì chúng cắt nhau tại một điểm trên trục toạ độ
Dưới đây là hướng dẫn giải các bài tập Tập 1 Bài 23 24 25 26 Tập 1 Trang 55 SGK Toán 9. Các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn lời giải đầy đủ và chi tiết Giải bài tập Đại số 9 trang 23 24 25 26 trang 55 SGK Toán 9 Bài 4 Trang 55. Các đường thẳng song song và cắt nhau trong Chương 2 – Hàm số bậc nhất dành cho các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 23 Trang 55 SGK Toán 9 Tập 1
Cho hàm số $y = 2x + b$. Xác định hệ số b cho từng trường hợp sau:
a) Đồ thị hàm số đã cho cắt trục tung tại tọa độ $-3$.
b) Đồ thị $ của hàm số đã cho đi qua điểm $a(1; 5).$
Giải pháp:
a) Đồ thị hàm số cắt trục tung tại điểm có hoành độ \(-3\) tức là đồ thị hàm số đi qua điểm (m(0; -3) ).
Thay thế \(x=0;\ y=-3\) vào công thức hàm \(y = 2x + b\) để được:
\(-3=2.0+b \leftrightarrow -3=0+ b \)
\(\leftrightarrow b=-3\)
Vậy \(b=-3\).
b) Thay thế \(x=1;\ y=5\) vào công thức hàm và nhận được:
\(5=2.1+b \leftrightarrow 5=2+b\)
\(\leftrightarrow 5-2 =b\) \(\leftrightarrow b=3\)
Vậy \(b=3\).
2. Giải bài 24 trang 55 SGK Toán 9 Tập 1
Cho hai hàm bậc nhất $y = 2x + 3k$ và $y = (2m + 1)x + 2k – 3.$
Điều kiện để tìm m và k là đồ thị của hai hàm này:
a) Hai đường thẳng cắt nhau.
b) Hai đường thẳng song song.
c) Hai đường thẳng trùng nhau.
Giải pháp:
Ta có:
\((d_{1}) \) \(y = 2x + 3k \rightarrow \left\{ \ma trận{ {a} = 2 \hfill \cr {b} = 3k \hfill \cr} \Có.\)
\((d_{2})\) \(y = \left( {2m + 1} \right)x + 2k – 3 \rightarrow \left\{ \ma trận { {a’} = 2m + 1 \hfill \cr {b’} = 2k – 3 \hfill \cr} \right.\)
Cho hai hàm số là hàm số bậc nhất khi và chỉ khi:
\(\left\{ \ma trận{ a \ne 0 \hfill \cr a’ \ne 0 \hfill \cr} \right. \leftrightarrow \left \{ \ma trận{ 2 \ne 0 \hfill \cr 2m + 1 \ne 0 \hfill \cr} \right \leftrightarrow \left\{ \ma trận{ 2 ne 0 \hfill \cr 2m \ne – 1 \hfill \cr} \right. \)
\(\leftrightarrow \left\{ \matrix{ 2 \ne 0 (luôn \ true) \hfill \cr m \ne \dfrac{-1}{2 } \hfill \cr} \Có.\)
a)Hai đường thẳng cắt nhau:
\((d_{1}) \) cắt \((d_{2}) \leftrightarrow a \ne a’\)
\(\leftrightarrow 2\neq 2m+1\) \(\leftrightarrow 2-1 \neq 2m\)
\(\leftrightarrow 1 \ne 2m\) \(\leftrightarrow m \ne \dfrac{1}{2}\)
Điều kiện của hàm bậc nhất kết hợp \(m \ne \pm \dfrac{1}{2}\).
b)Hai đường thẳng song song:
\((d_{1}) // (d_{2}) \leftrightarrow \left\{\begin{matrix} a=a’ \\ b\neq b’ end{Ma trận}\Có.\)
\(\leftrightarrow \left\{\begin{ma trận} 2=2m+1\\ 3k\neq 2k-3 \end{ma trận}\right.\)
\(\leftrightarrow \left\{\begin{ma trận} 2-1=2m\\ 3k-2k\neq -3 \end{ma trận}\right.\ )
\(\leftrightarrow \left\{\begin{matrix} m=\dfrac{1}{2} (hài lòng\ hài lòng)\\ k\neq -3 \ cuối{ma trận}\ngay.\)
Vậy \(m=\dfrac{1}{2}\) và \( k \ne -3\) thì hai đồ thị song song.
c)Hai dòng trùng nhau:
\((d_{1})\) \(\equiv\) \((d_{2}) \leftrightarrow\) \(\left\{ \ begin{matrix} a=a’ \\ b=b’ \end{matrix} \right.\)
\(\leftrightarrow \left\{\begin{ma trận} 2=2m+1\\ 3k= 2k-3 \end{ma trận}\right.\)
\(\leftrightarrow \left\{\begin{matrix} 2-1=2m\\ 3-2k= -3 \end{matrix}\right.\)
\(\leftrightarrow \left\{\begin{matrix} 2m=1 \\ k=-3 \end{matrix}\right.\)
\(\leftrightarrow \left\{\begin{matrix} m=\dfrac{1}{2}(tm) \\ k= -3 \end{matrix} Có.\)
Vậy \(m=\dfrac{1}{2}\) và \(k=-3\) thì đồ thị của hai hàm số này bằng nhau.
3. Giải bài 25 trang 55 SGK Toán 9 Tập 1
a) Vẽ các hàm sau trên cùng một mặt phẳng tọa độ:
$y = \frac{2}{3}x + 2; y = -\frac{3}{2}x + 2.$
b) Một đường thẳng song song với trục hoành ox, cắt trục tung oy tại điểm bằng 1, cắt đường thẳng $y = \frac{2}{3}x + 2$ và $y = – \frac{3}{2}x + 2$ lần lượt tại hai điểm m và n. Tìm tọa độ hai điểm m và n.
Giải pháp:
a) Hàm \(y = \dfrac{2}{3}x + 2\)
Cho \(x= 0 \rightarrow y = \dfrac{2}{3}.0+ 2=0+2=2 \rightarrow a(0; 2)\)
Đối với \(y= 0 \rightarrow 0 = \dfrac{2}{3}.x+ 2 \rightarrow x=-3 \rightarrow c(-3; 0)\)
Đường thẳng đi qua hai điểm \(a,\ c\) là đồ thị của hàm số \(y = \dfrac{2}{3}x + 2\).
+) hàm \(y =- \dfrac{3}{2}x + 2\)
Cho \(x= 0 \rightarrow y = -\dfrac{3}{2}.0+ 2=0+2=2 \rightarrow a(0; 2)\)
Cho \(y=0 \rightarrow y = -\dfrac{3}{2}.0+ 2 \rightarrow x= \dfrac{4}{3} \rightarrow b {\ Trái(\dfrac{4}{3}; 0 \phải)}\)
Đường thẳng đi qua hai điểm \(a,\ b\) là đồ thị của hàm số \(y = -\dfrac{3}{2}x + 2\).
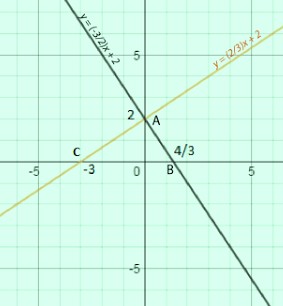
b) Một đường thẳng song song với trục \(ox\) cắt trục \(oy\) tại một điểm có tọa độ \(1\): (y=1\).
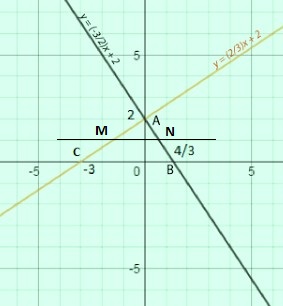
Vì \(m\) là giao điểm của đường thẳng \(y=\dfrac{2}{3}x+2\) và \(y=1\)\( m ) là nghiệm của phương trình:
\(\dfrac{2}{3}x+2=1\) \(\leftrightarrow \dfrac{2}{3}x=1-2\)
\(\leftrightarrow \dfrac{2}{3}x=-1\) \(\leftrightarrow x=-\dfrac{3}{2}\)
Vậy tọa độ \(m\) là: \(m{\left( -\dfrac{3}{2}; 1 \right)}\).
Vì \(n\) là giao điểm của đường thẳng \(y=-\dfrac{3}{2}x+2\) và \(y=1\) nên vậy\ Tọa độ của (n\) là nghiệm của phương trình:
\(-\dfrac{3}{2}x+2=1\) \(\leftrightarrow -\dfrac{3}{2}x=1-2\)
\(\leftrightarrow -\dfrac{3}{2}x=-1\) \(\leftrightarrow x=\dfrac{2}{3}\)
Vậy tọa độ \(n\) là: \(n{\left( \dfrac{2}{3}; 1 \right)}\).
4. Giải bài 26 trang 55 SGK Toán 9 Tập 1
Đối với hàm bậc nhất $y = ax – 4 (1)$. Xác định hệ số a cho từng trường hợp sau:
a) Đồ thị hàm số $(1)$ cắt đường thẳng $y = 2x – 1$ tại điểm có tọa độ $2$.
b) Đồ thị hàm số $(1)$ cắt đường thẳng $y = -3x + 2$ tại điểm có tọa độ $5$.
Giải pháp:
a)Xét phương trình tọa độ giao điểm: \(ax-4=2x-1\).
Thay \(x=2\) vào công thức trên, ta được: ;
\(a.2-4=2.2-1\)
\(\leftrightarrow 2a=4-1+4\) \(\leftrightarrow a=\dfrac{7}{2}\).
b) Ta có: \((1)\) \(y = ax – 4\)
\((2)\) \(y = -3x +2 \)
Thay tọa độ giao điểm vào phương trình\((2)\) ta được:
\(5=-3.x+2\) \( \leftrightarrow 5-2 = -3x\)
\(\leftrightarrow 3=-3x\) \(\leftrightarrow x=-1\)
Vậy tọa độ giao điểm là \(x=-1\). Thay \(x=-1,\ y=5\) vào phương trình \((1)\) ta được:
\(5=a.(-1) – 4\) \(\leftrightarrow 5+4=-a\)
\(\leftrightarrow -a=9\) \(\leftrightarrow a=-9\)
Vậy \(a=-9\).
Trước:
- Giải bài 20 21 22 trang 54 55 SGK Toán 9 Tập 1
- Giải bài trang 27 và trang 58 SGK Toán 9 tập 1
- Câu hỏi khác 9
- Học tốt vật lý lớp 9
- Học tốt môn sinh học lớp 9
- Học tốt ngữ văn lớp 9
- Điểm tốt môn lịch sử lớp 9
- Học tốt môn địa lý lớp 9
- Học tốt tiếng Anh lớp 9
- Tiếng Anh lớp 9 thí điểm
- Học Khoa học Máy tính Lớp 9
- Học tốt GDCD lớp 9
Tiếp theo:
Xem thêm:
<3
“Môn thể thao nào đã khó giabaisgk.com”
