Đọc 4 tính chất về ba đường trung tuyến của một tam giác: Giải bài 23,24 trang 66; bài 25,26,27,28,29,30 trang 67 sgk toán 7 tập 2 chương 3 hình học.
23. Gọi g là trọng tâm của Δdef và đường trung trực là dh. Khẳng định nào sau đây là đúng?
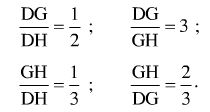
g là trọng tâm và trung tuyến dh của Δdef. Phát biểu đúng là:
24. cho hình ảnh hồ sơ. Điền số thích hợp vào chỗ trống trong các đẳng thức sau:
a) mg = … ông ; gr = … ông; gr = … mg
b) ns = ..ng; ns = …gs; ng = gs
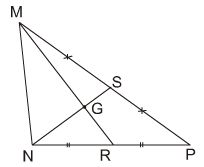
Hình vẽ cho chúng ta biết hai đường trung trực mr và ns cắt nhau tại g nên g là trọng tâm của tam giác. Vì vậy, chúng tôi nhập các số như sau:
Bài 25, trang 67. Biết: Trong hình vuông, trung tuyến của cạnh bằng nửa cạnh huyền. Vui lòng giải quyết các vấn đề sau:
Vì Δvuông abc có hai cạnh ab = 3cm, ac = 4cm. Tính khoảng cách từ đỉnh a đến trọng tâm g của abc.
Giải thích:Δabc vuông tại a =>; bc2 = ab2 + ac2
bc2 = 32 + 42
bc2 = 25
bc = 5
Gọi m là trung điểm của bc => am là trung trực của nửa cạnh huyền nên am = 1/2 bc
Vì g là trọng tâm của abc nên:
26. Chứng minh định lý: Trong một mặt phẳng cân, đường trung trực của hai cạnh bằng nhau.
Giả sử abc cân tại a, có hai trung tuyến bm và cn, ta chứng minh bm = cn
Ta có an = nb = ab/2 (thuộc tính của đường giữa)
am = mc = ac/2 (thuộc tính đường giữa)
Vì ∆ abc cân tại a=> ab = ac nên am = an
Xem bam ;Δ có thể có:
am = an (cm)
Góc bình thường
ab = ac(Δabc cân)
Có nên suy ra bam = can (c-g-c)
=> bm = cn (2 cạnh tương ứng)
bài 27.Chứng minh nghịch đảo của định lý trên: Nếu Δ có hai trung tuyến bằng nhau thì cân.
Giả sử abc có hai trung tuyến be và cf cắt nhau tại g
=>g là trọng tâm của
=>gb = 2/3 đúng; GC = 2/3 cf
tức là be = cf (giả sử) nên gb = gc
=> Δgbc cân gcb = gbc tại g => gt;
Xem xét bgf và cge với:
gb = gc (cmt)
Góc bgf = góc cge (2 góc đối đỉnh)
ge=gf
⇒ bgf = cge (c-g-c)
⇒ bf = ce (tương ứng 2 vế)
Xét Δfbc và Δecb trong đó bf = ce (cmt) cạnh bc chung be = cf (gt)
⇒ Δfbc = Δecb(c-c-c) ⇒ góc b = góc c vì Δabc có góc b = góc c ⇒ Δabc là Δ cân tại a. (2 góc ở đáy bằng nhau)
Sau 28.Vì Δdef bằng d và trung vị di
a) Chứng minh rằng dei = dfi
b) Góc die và dif là gì?
c) Biết de = df = 13cm, ef = 10cm, tính độ dài đường trung tuyến.
Giải:a) ∆dei = ∆dfi có:
di là mặt chung
de = df (số dư nợ)
tức là = nếu (di là median.line)
=> Δdei = Δdfi (c.c.c)
b) Vì Δdei = Δdfi =>cái chết=sự khác biệt
die + dif= 1800 (liền kề)
do diem = dif = 900
c) i là trung điểm của ef nên ie = if = 5cm
Δdei bình phương tại i => di2 = de2 – ei2 (định lý pytagogue)
=> di2 = 132 – 52 = 144
=> di = 12
Bài 29, trang 67. Gọi g là trọng tâm của Δmọi abc. Bằng chứng:
ga =gb = gc
Cho m, n, e là giao điểm của ag, bg, cg và bc, ca, ab.
Vì g là trọng tâm của abc
Vì Δabc đều nên ba giá trị trung tuyến của các đường thẳng ứng với ba cạnh bc, ca, ab đều bằng nhau
=>am = bn = ce (2)
Từ (1), (2) => ga = gb = gc
Bài 30 trang 67 Toán 7: Gọi g là trọng tâm của Δabc. Lấy điểm g’ trên tia ag sao cho g là trung điểm của ag’
a) So sánh biên của bgg’ với trung vị của Δabc
b) So sánh trung tuyến của Δbgg’ với các cạnh của Δabc.
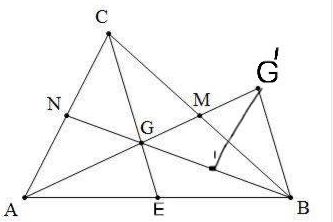
a) So sánh cạnh của bgg’ với trung tuyến của abc bg cắt nhau tại n ac
cg cắt ab tại e
g là trọng tâm của abc
=>ga = 2/3 sáng
ga = gg’ (g là trung điểm của ag’)
gg’ = 2/3 giờ sáng
Vì g là trọng tâm của ∆abc => gb = 2/3 tỷ
Ngược lại: gm = 1/2 ag (g là trọng tâm)
ag = gg’ (gt)
gm = 1/2 gam’
m là trung điểm gg’
Vậy gmc = g’mb vì:
gram=mg’
mb = mc
∠gmc = g’mb
=>bg’ = cg
trong đó cg = 2/3 ce (g là trọng tâm abc)
=> bg’ = 2/3 ce
Vậy mỗi cạnh của bgg’ bằng 2/3 trung tuyến của Δabc
b) So sánh trung tuyến của ∆bgg’ với cạnh ∆abc
Ta có: bm là đường trung bình của bgg’
với m là trung điểm của bc nên bm = 1/2 bc
Vì ig = 1/2 bg (i là trung điểm của bg)
gn = 1/2 bg (g là trọng tâm)
=>ig = gn
Do đó ∆igg’ = ∆nga (cgc) => ig’ = a => ig’ = ac/2
– Gọi k là trung điểm bg => gk là trung tuyến ∆bgg’
Vì ge = 1/2 gc (g là trọng tâm abc)
=>ge = 1/2 bg
với k là trung điểm bg’ => kg’ = eg
Vì gmc = g’bm (đã chứng minh ở trên)
=> ∠gcm = ∠g’bm (góc đáy nội tiếp lại)
=>ce // bg’ => age = ag’b(isotope)
Do đó ∆age = ∆gg’k (cgc) => ae = gk
ae = 1/2 ab nên gk = 1/2 ab
Vậy mỗi đường trung tuyến bgg’ bằng một nửa các cạnh song song của abc
