Vật lý 12 Bài 1: Dao động điều hòa – HOC247

Dao động cơ là sự chuyển động qua lại của một vật quanh vị trí cân bằng.

Dao động tuần hoàn là dao động mà cứ sau những khoảng thời gian bằng nhau gọi là chu kì thì vật lại trở về vị trí cũ theo phương cũ. Dao động tuần hoàn đơn giản nhất là dao động điều hòa.

A. Ví dụ về cộng hưởng

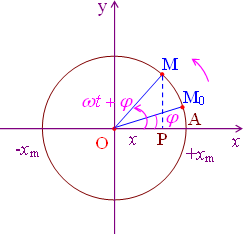
• Giả sử m chuyển động tịnh tiến thì vận tốc góc \(\omega, p\) là hình chiếu của m lên ox.

  • Tại t = 0, m có tọa độ góc \(\varphi\)

  • Sau thời điểm t, m có tọa độ góc \(\varphi+\omega t\)

  • Sau đó: \(\overline{op}\) = \(x\); \(x=omcos(\omega t+\varphi)\)

  • Nhập a = om ta được: \(x=acos(\omega t+\varphi)\)

  • trong đó \(a, \omega, \varphi\) là các hằng số

  • Vì hàm cosin là hàm điều hòa nên điểm p gọi là điểm dao động điều hòa.

    b. Định nghĩa dao động điều hòa

    • Dao động điều hòa là dao động trong đó độ dời của vật là một hàm của cosin (hoặc sin) của thời gian.

      c. phương trình

      • Phương trình \(x = acos(\omega t + \varphi)\) được gọi là phương trình dao động điều hòa.

        • a là biên độ, tức là độ dời lớn nhất của vật, a >;0.

        • \(\omega t + \varphi\) là pha của dao động tại thời điểm t

        • \(\varphi\) là pha ban đầu tại t = 0 (\(\varphi\) 0, \ (\varphi\) = 0)

          d.Làm theo

          • Điểm p trên một đoạn thẳng dao động điều hòa luôn được coi là hình chiếu của một điểm m chuyển động tròn đều trên đường kính của đoạn thẳng đó.

          • Như thường lệ, chúng ta chọn trục x làm gốc để tính pha dao động, và chiều tăng pha tương ứng với góc \(\widehat{mop }\) để thực hiện chuyển động tròn đều.

            A. khoảng thời gian và tần suất

            • Khi vật trở về vị trí và phương ban đầu, ta nói vật thực hiện một dao động toàn phần.

              • Chu kỳ (t): Dao động điều hòa là thời gian để vật thực hiện được một dao động toàn phần. đơn vị là s

              • Tần số (f): Dao động điều hòa là số dao động tuần hoàn xảy ra trong một giây. Đơn vị là 1/s hoặc hz.

                b. Tần số góc

                • Trong dao động điều hòa, \(\omega\) được gọi là tần số góc.

                • Có mối quan hệ giữa tần số góc, chu kỳ và tần số: \(\omega = \frac{2\pi}{t}=2\pi f\)

                  A. Tốc độ

                  • Vận tốc là đạo hàm của độ dời theo thời gian.

                    \(v=x’= – \omega asin (\omega t+\varphi)\)

                    • Vận tốc cũng thay đổi theo thời gian.

                      • Tại \(x=\pm a\) thì \(v = 0\)

                      • Tại \(x = 0\) thì \(v = v_{max} = \omega a\)

                        Gia tốc

                        • Gia tốc là đạo hàm của vận tốc theo thời gian

                          \(a=v’=x{}”= – \omega^2 acos (\omega t+\varphi)\)

                          \(a= – \omega^2 x\)

                          • Tại \(x=0\) thì \(a = 0\)

                          • Tại \(x=\pm a\) rồi \(a=a_{max}=\omega^2a\)

                            

                            \(\varphi= 0\) Đồ thị dao động điều hòa có dạng hình sin nên còn gọi là dao động điều hòa.