Kiến thức nổi bật và hướng dẫn giải bài 75,76, 77, 78,79, 80, 81,82,83 trang 33 toán 8 tập 1: ôn tập chương 1 – đại số 8.</strong
A. Lý thuyết Chương 1 Đại số 8 Tập 1.
1.Nhân đơn thức với đa thức. a.(b+c) = ab+ac
2.Đa thức nhân với đa thức. (a+b)(c+d) = ac+ad+bc+bd
3. Bảy hằng đẳng thức khó quên.
4.Chia đơn thức cho đơn thức.
5.Chia đa thức cho đơn thức.
6.Chia đa thức cho đa thức.
———
Ôn tập Đại số 8 chương 1 có 5 bài tập các em cần nhớ:
Dạng 1: Các phép tính (câu 75, 76, 77, 80) Dạng 2: Rút gọn biểu thức 78 Dạng 3: Bài toán chia nhân tử cho đa thức 78 Dạng 4: Bài toán tìm x (câu 81) Dạng 5: Chứng minh rằng… (bài 82)
b. Hoàn thành bài tập ôn tập chương 1 Toán, Đại số 1 trang 33.
75 sau. Phép nhân:
a) 5×2.(3×2 – 7x + 2)
b) 2/3xy( 2x2y – 3xy + y2)
Giải pháp:
a) 5×2.(3×2 – 7x + 2) = 15×4 – 35×3 + 10×2
b) 2/3xy( 2x2y – 3xy + y2) = 4/3x3y2 – 2x2y2 + 2/3 xy3
Bài tập 76. Phép nhân:
a) (2×2 – 3x)(5×2 – 2x + 1)
b)(x – 2y)(3xy + 5y2 + x)
HD: a) (2×2 – 3x)(5×2 – 2x + 1) = 2×2(5×2 – 2x + 1) – 3x(5×2 – 2x + 1)
= 10×4 – 4×3 + 2×2 – 15×3 + 6×2 – 3x = 10×4 – 19×3 + 8×2 – 3x
b) (x – 2y)(3xy + 5y2 + x) = x(3xy + 5y2 + x) – 2y(3xy + 5y2 + x)
= 3x2y + 5xy2 + x2 – 6xy2 – 10y3 – 2xy = 3x2y – xy2 + x2 – 10y3 – 2xy
bài 77.Tính nhanh giá trị biểu thức:
a) m = x2 + 4y2 – 4xy tại x = 18 và y = 4
b) n = 8×3 – 12x2y + 6xy2 – y3 tại x = 6 và y = -8
HD: a) m = x2 + 4y2 – 4xy = x2 – 4xy + 4y2 = x2 – 2.x(2y) + (2y)2 = (x – 2y)2 tại x = 18 và y = 4 thì m = (18 – 2,4)2 = 102 = 100
b) n = 8×3 – 12x2y + 6xy2 – y3 = (2x)3 – 3.(2x)2y + 3.2x.y2 – y3 = (2x – y)3 tại x = 6 và y = -8 thì n = (2,6 + 8)3 = 203 = 8000
bài 78. Rút gọn biểu thức sau:
a) (x + 2)(x – 2) – (x – 3) (x + 1)
b) (2x + 1)2 + (3x – 1)2 + 2(2x +1)(3x – 1)
Giải:a) (x + 2)(x – 2) – (x – 3)(x + 1) = (x2 – 22) – (x2 + x – 3x – 3 ) =-x2 – 4 -x2 – x + 3x + 3 = 2x – 1
b) (2x + 1)2 + (3x – 1)2 + 2(2x +1)(3x – 1) = (2x + 1)2 + 2(2x + 1)(3x – 1) + (3x – 1)2
= [(2x + 1) + (3x – 1)]2 = (2x + 1 + 3x – 1)2 = (5x)2 = 25×2
Sau 79. Rút gọn đa thức sau:
a) x2 – 4 + (x – 2)2
b) x3 – 2×2 + x – xy2
c) x3 – 4×2 – 12x + 27
Giải:a) x2 – 4 + (x – 2)2 = (x2 – 22) + (x – 2)2 = (x – 2)(x + 2) + ( x – 2)2 = (x – 2) [(x + 2) + (x – 2)] = (x – 2)(x + 2 + x – 2) = 2x(x – 2)
b) x3 – 2×2 + x – xy2 = x(x2 – 2x + 1 – y2) = x[(x2 – 2x + 1) – y2]
= x[(x – 1)2 – y2] = x[(x – 1) + y] [(x – 1) – y] = x(x – 1 + y)(x – 1 – y )
c) x3 – 4×2 – 12x + 27 = (x3 + 27) – 4x(x + 3) = (x + 3)(x2 – 3x + 9) – 4x(x + 3)
= (x + 3)(x2 – 3x + 9 – 4x) = (x + 3)(x2 – 7x + 9)
Những năm sau thập niên 80. Thực hiện phép chia:
a) (6×3 – 7×2 – x + 2): (2x + 1)
b) (x4 – x3 + x2 + 3x): (x2 – 2x + 3)
c) (x2 – y2 + 6x + 9) : (x + y + 3)
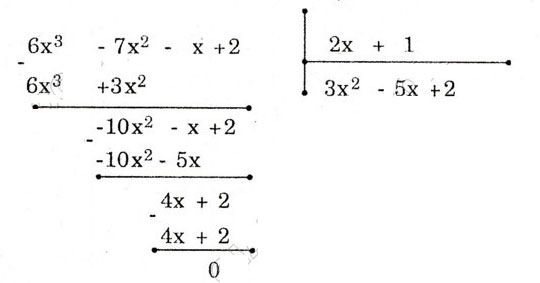
Khi đó: (6×3 – 7×2 – x + 2) : (2x + 1) = 3×2 – 5x + 2
b) (x4 – x3 + x2 + 3x): (x2 – 2x + 3)
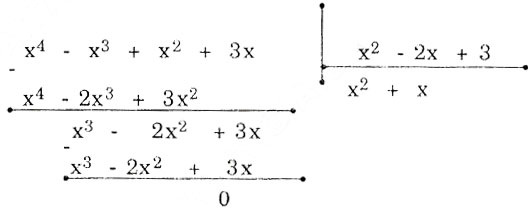
Khi đó (x4 – x3 + x2 + 3x): (x2 – 2x + 3) = x2 + x
(x2 – y2 + 6x + 9) : (x + y + 3) = (x2 + 6x+ 9) – y2 : (x + y + 3)
=(x + 3)2 – y2 : (x + y + 3) = (x + 3 – y) (x + 3 + y) : (x + y + 3) = (x – y + 3 )
bài 81 toán 8 tập 1.Tìm x biết:
a) 2/3x(x2 – 4) = 0
b) (x + 2)2 – (x – 2)(x + 2) = 0
c) x + 2√2×2 + 2×3 = 0
Đáp án:a) 2/3x(x2 – 4) = 0 ⇔ 2/3x(x – 2)(x + 2) = 0 ⇔ x = 0 hoặc x – 2 = 0 hoặc x + 2 = 0 ⇔ x = 0 hoặc x =2 hoặc x = -2
b) (x + 2)2 – (x – 2)(x + 2) = 0 ⇔ (x + 2)[(x + 2) – (x – 2)] = 0 ⇔ 4(x + 2) = 0 x + 2 = 0 x = -2
c) x + 2√2×2 + 2×3 = 0 ⇔ x(1 + 2√2x + 2×2) = 0 ⇔ x(1 + √2x)2 = 0
Hoặc x = 0 hoặc (1 + √2x)2= 0 ⇔ 1 + √2x = 0 ⇔ x =-1/√2
Sau năm 82.Bằng chứng:
a) x2- 2xy + y2 + 1 > 0 với mọi số thực x và y
b) x – x2 – 1 <; 0 với mọi số thực x
Đáp án:a) Ta có: x2 – 2xy + y2 = (x – y)2 > 0 với mọi số thực x và y
⇒ x2 – 2xy + y2 + 1 = (x – y)2 +1 > 1 ⇒ (x – y)2 +1 > 0 với mọi số thực x và y
b) Ta có: x – x2 – 1 = -(x2 – x + 1) = – (x2-2.½x + ¼ + ¾) = – (x2-2.½x + ¼) – ¾ = – (x -½)2 – ≤ – với mọi số thực x.
⇒ x – x2 – 1 = – (x -½)2 – ¾ ≤ 0 với mọi số thực x.
bài 83 trang 33 toán 8: Tìm n ∈ z sao cho 2n2 – n + 2 chia hết cho 2n +1.
Ta có: 2n2 – n + 2 : (2n + 1)
Ta có: n ∈ z và 2n2 – n + 2 chia hết cho 2n + 1 thì 2n + 1 chia hết cho 3. Các ước của 3 là ±1; ± 3
- Khi 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
- Khi 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
- Khi 2n + 1 = 3 2n = 2 ⇔ n – 1
- Khi 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2
Do đó, n = 0 hoặc n = -1 hoặc n = 1 hoặc n = -2.
