Bài tập 1 trang 88 SGK hình học
Xác định độ dài trục, tọa độ tiêu điểm, tọa độ đỉnh và vẽ hình elip theo các phương trình sau:
a) \(\frac{x^{2}}{25} + \frac{y^{2}}{9}= 1\)
b) \(4x^2+ 9y^2= 1\)
c) \(4x^2+ 9y^2= 36\)
NGƯỜI CHIẾN THẮNG
a) Ta có: \(a^2= 25 \rightarrow a = 5\) độ dài của trục chính \(2a = 10\)
\( b^2= 9 \rightarrow b = 3\) chiều dài trục nhỏ \(2a = 6\)
\(c^2= a^2- b^2= 25 – 9 = 16 \mũi tên bên phải c = 4\)
Vậy hai tiêu điểm là: \(f_1(-4 ; 0)\) và \(f_2(4 ; 0)\)
Tọa độ đỉnh\(a_1(-5; 0), a_2(5; 0), b_1(0; -3), b_2(0; 3)\).
hai)
\(4x^2+ 9y^2= 1\leftrightarrow \frac{x^{2}}{\frac{1}{4}} + \frac{y^{2}} {\frac{1}{9}} = 1\)
\(a^2 =\frac{1}{4}\rightarrow a = \frac{1}{2}\) \(\rightarrow\) chiều dài trục chính (2a = 1\)
\(b^2= \frac{1}{9}\rightarrow b = \frac{1}{3}\) \(\rightarrow\) Độ dài trục nhỏ (2b = \frac{2}{3}\)
\(c^2= a^2- b^2= \frac{1}{}4- \frac{1}{9} = \frac{5}{36}\) \(\rightarrow c = \frac{\sqrt{5}}{6}\)
\(f_1(-\frac{\sqrt{5}}{6} ; 0)\) và \(f_2(\frac{\sqrt{5}}{6} ; 0)\)
\(a_1(-\frac{1}{2}; 0), a_2(\frac{1}{2}; 0)\), \(b_1(0; -\ frac{1}{3} ), b_2(0; \frac{1}{3} )\).
c) Chia vế \(2\) của phương trình cho \(36\) ta được:
\(\frac{x^{2}}{9}+ \frac{y^{2}}{4}= 1\)
Suy ra từ đây: \(2a = 6, 2b = 4, c = \sqrt5\)
Suy ra \(f_1(-\sqrt5 ; 0)\) và \(f_2(\sqrt5 ; 0)\)
\(a_1(-3; 0), a_2(3; 0), b_1(0; -2), b_2(0; 2)\).
bài giảng 2 trang 88 SGK Hình Học 10
Lập phương trình chính tắc của hình elip và biết:
a) Trục chính và trục phụ là \(8\) và \(6\)
b) Trục chính bằng \(10\) và tiêu cự bằng \(6\)
NGƯỜI CHIẾN THẮNG
Phương trình chính tắc của hình elip có dạng sau:
\(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
a) Ta có \(a > b\):
\(2a = 8 \rightarrow a = 4 \rightarrow a^2= 16\)
\(2b = 6 \rightarrow b = 3 \rightarrow b^2= 9\)
Vậy phương trình chính tắc của hình elip có dạng \(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{9} ) = 1
b) Ta có: \(2a = 10 \rightarrow a = 5 \rightarrow a^2= 25\)
\(2c = 6 \rightarrow c = 3 \rightarrow c^2= 9\)
\(\rightarrow b^2=a^2-c^2 \rightarrow b^2= 25 – 9 = 16\)
Khi đó phương trình chính tắc của hình elip có dạng \(\frac{x^{2}}{25} + \frac{y^{2}}{16}= 1\)
Bài 3 Trang 88 SGK Hình học 10
Dựng phương trình chính tắc của hình elip khi:
a) Hình elip đi qua các điểm \(m(0; 3)\) và \(n( 3; \frac{-12}{5})\)
b) Một tiêu điểm là \(f_1( -\sqrt3; 0)\) và một điểm \(m(1; \frac{\sqrt{3}}{2}) ) trên hình elip
NGƯỜI CHIẾN THẮNG
Phương trình chính tắc của hình elip có dạng: \(\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2 } } = 1\)
a) Hình elip đi qua \(m(0; 3)\)
\(\frac{0^{2}}{a^{2}} + \frac{3^{2}}{b^{2}}= 1 \rightarrow b^2= 9\)
Hình elip đi qua \(n( 3; \frac{-12}{5})\)
\(\frac{3^{2}}{a^{2}} + \frac{\left(\frac{-12}{5}\right)^{2} }{9} = 1 \mũi tên phải a^2= 25\)
Phương trình chính quy của hình elip là: \(\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1\)
b) Ta có: \(c = \sqrt3 \rightarrow c^2= 3\)
Elip đi qua điểm \(m(1; \frac{\sqrt{3}}{2})\)
\(\frac{1}{a^{2}} + \frac{\left(\frac{\sqrt{3}}{2}\right)^{2} }{b^{2}}= 1 \rightarrow \frac{1}{a^{2}}+ \frac{3}{4b^{2}}= 1\) (1)
Ngược lại: \( c^2=a^2-b^2\)
\(\rightarrow 3 = a^2-b^2\rightarrow a^2=b^2 + 3\)
Thay (1) ta được: \(\frac{1}{b^{2}+ 3} + \frac{3}{4b^{2}} = 1\)
\(\mũi tên phải a^2= 4b^2+ 5b^2- 9 = 0 \)
\(\rightarrow b^2 =1\) hoặc \( b^2= \frac{-9}{4}\) (loại)
sử dụng \( b^2= 1\rightarrow a^2= 4\)
Phương trình chính tắc của hình elip là: \(\frac{x^{2}}{4} + \frac{y^{2}}{1}= 1\)
Bài 4 Trang 88 SGK Hình Học 10
Để cắt một biển quảng cáo hình bầu dục có trục chính \(80cm\) và trục phụ\(40 cm\) từ một tấm ván ép hình chữ nhật có kích thước \( 80cm \ nhân 40cm\), một là Vẽ một hình elip trên bảng đen, như trong Hình 3.19. Hai chiếc đinh phải đóng cách mép của tấm gỗ dán bao xa và vòng dây phải dài bao nhiêu?
NGƯỜI CHIẾN THẮNG
Ta có: \(2a = 80 \rightarrow a = 40\)
\(2b = 40\mũi tên phải b = 20\)
\( c^2= a^2- b^2= 1200 \rightarrow c = 20\sqrt 3\)
Phải được đóng đinh tại điểm \(f_1, f_2\) và khoảng cách từ mép ván:
\(f_2a = oa – of_2= 40 – 20\sqrt3\)
\(\rightarrow f_2a = 20(2 – \sqrt3) ≈ 5,4cm\)
Chu vi của dây bằng: \(f_1f_2+ 2a = 40\sqrt 3 + 80\)
\(\rightarrow f_1f_2+2a = 40(2 + \sqrt 3)\)
\( f_1f_2+ 2a ≈ 149,3cm\)
Bài 5 SGK Hình học, Trang 88
Cho hai vòng tròn \({c_1}({f_1};{r_1})\) và \({c_2}({f_2};{r_2})\). \(c_1\) trong \(c_2\) và \(f_1≠ f_2\). Đường tròn biến thiên \((c)\) luôn tiếp xúc với \(c_1\) ở bên ngoài và \(c_2\) ở bên trong. Cho biết tâm của đường tròn \(m\) ((c)\) di chuyển trên hình elip.
NGƯỜI CHIẾN THẮNG
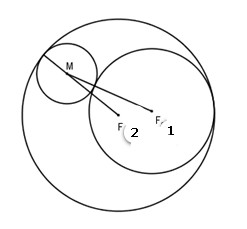
Gọi \(r\) là bán kính của đường tròn\((c)\)
\((c)\) và \(c_1\) là các liên kết bên ngoài, mang lại cho chúng ta:
\(mf_1= r_1+ r\) (1)
\((c)\) và \(c_2\) được liên kết với nhau, cho chúng ta:
\(mf_2= r_2- r\) (2)
Từ (1) và (2) ta có
\(m{f_1} + m{f_2} = {r_1} + {r_2} = r\) không thay đổi
Tổng khoảng cách từ điểm m đến hai điểm cố định \(f_1\) và \(f_2\)\(m{f_1} + m{f_2}\) bằng không thay đổi ({ r_1} + {r_2}\)
Vậy tập hợp điểm \(m\) là một hình elip có tiêu điểm \(f_1\) và \(f_2\) và có tiêu cự
\(f_1f_2= r_1+r_2\)
giaibaitap.me
