Giải bài 34,35,36,37,38 trang 56, bài 39,40 trang 57 SGK Toán 9 Tập 2: Phương Trình Bậc Hai – Chương 4.
Lưu ý: viết tắt phương trình thành pt
bài 34. Giải pháp song song:
a) x4 – 5×2 + 4 = 0; b) 2×4 – 3×2 – 2 = 0;
c) 3×4 + 10×2 + 3 = 0
HD: a) x4 – 5×2+ 4 = 0.
Giả sử x2 = t ≥ 0, ta có: t2 – 5t + 4 = 0; t1 = 1, t2 = 4
Nên: x1 = -1, x2 = 1, x3 = -2, x4 = 2.
b) 2×4 – 3×2 – 2 = 0.
Giả sử x2 = t ≥ 0, ta có: 2t2 – 3t – 2 = 0; t1 = 2, t2 = -1/2 (loại)
Vậy: x1 = √2; x2 = -√2
c) 3×4 + 10×2 + 3 = 0.
Giả sử x2 = t ≥ 0, ta có: 3t2 + 10t + 3 = 0; t1 = -3(loại),
t2 = -1/3 (loại)
pt vô nghiệm
bài 35. Giải quyết vấn đề:
HD:
⇔ x2 – 9 + 6 = 3x – 3×2
⇔ 4×2 – 3x – 3 = 0; = 57
Điều kiện x ≠ 2, x 5.
(x + 2)(2 – x) + 3(x – 5)(2 – x) = 6(x – 5)
⇔ 4 – x2 – 3×2 + 21x – 30 = 6x – 30 ⇔ 4×2 – 15x – 4 = 0
∆ = 225 + 64 = 289, = 17
Điều kiện: x≠-1; x-2
pt tương đương: 4(x + 2) = -x2 – x + 2
⇔ 4x + 8 = 2 – x2 – x
⇔ x2 + 5x + 6 = 0
Giải ta được: x1 = -2 không thỏa mãn điều kiện của ẩn nên pt có duy nhất một nghiệm x = -3.
bài 36. Giải quyết vấn đề:
a) (3×2 – 5x + 1)(x2 – 4) = 0;
b) (2×2 + x – 4)2 – (2x – 1)2 = 0
HD:a) (3×2 – 5x + 1)(x2 – 4) = 0
=> 3×2 – 5x + 1 = 0
hay x2 – 4 = 0 => x = ±2.
b) (2×2 + x – 4)2 – (2x – 1)2 = 0
⇔ (2×2 + x – 4 + 2x – 1)(2×2 + x – 4 – 2x + 1) = 0
⇔ (2×2 + 3x – 5)(2×2 – x – 3) = 0
=> 2×2 + 3x – 5 = 0 hoặc 2×2 – x – 3 = 0
x1 = 1; x2 = -2,5; x3 = -1; x4 = 1,5
bài 37.trùng hợp gpt:
a) 9×4 – 10×2 + 1 = 0; b) 5×4 + 2×2 – 16 = 10 – x2;
c) 0,3×4 + 1,8×2 + 1,5 = 0; đ) 2×2 + 1 = 1/x² – 4
hd: a) 9×4 – 10×2 + 1 = 0. Gọi t = x2 ≥ 0, ta có: 9t2 – 10t + 1 = 0.
Vì a + b + c = 9 – 10 + 1 = 0 nên t1 = 1, t2 = 1/9
Suy ra: x1 = -1, x2 = 1, x3 = -1/3 , x4 = 1/3
b) 5×4 + 2×2 – 16 = 10 – x2 ⇔ 5×4 + 3×2 – 26 = 0.
Giả sử t = x2 ≥ 0, ta có: 5t2 + 3t -26 = 0
∆ = 9 + 4. 5. 26=529=232;t1=2,t2=-2,6 (loại). Vậy: x1 = 2, x2 = -√2
c) 0,3×4 + 1,8×2 + 1,5 = 0 ⇔ x4 + 6×2 + 5 = 0. Cho t = x2 ≥ 0, ta có:
t2 + 6t + 5 = 0, t1 = -1 (loại), t2 = -5 (loại)
pt không có nghiệm,
Chú ý: Cũng có thể ghi x4 + 6×2 + 5 ≥ 5 ở bên trái, 0 ở bên phải nên pt vô nghiệm.
Điều kiện x 0
2×4 + 5×2 – 1 = 0. Cho t = x2 ≥ 0, ta có:
2t2 + 5t – 1 = 0; = 25 + 8 = 33
Bài 38 Toán 9. Giải phương trình:
a) (x – 3)2 + (x + 4)2 = 23 – 3x;
b) x3 + 2×2 – (x – 3)2 = (x – 1)(x2 – 2);
HD:a) (x – 3)2 + (x + 4)2 = 23 – 3x ⇔ x2 – 6x + 9 + x2 + 8x + 16 = 23 – 3x
⇔ 2×2 + 5x + 2 = 0
∆ = 25 – 16 = 9
x1 = -2, x2 = -1/2
b) x3 + 2×2 – (x – 3)2 = (x – 1)(x2 – 2)
⇔ x3 + 2×2 – x2 + 6x – 9 = x3 – x2 – 2x + 2 ⇔ 2×2 + 8x – 11 = 0
Δ’ = 16 + 22 = 38
c) (x – 1)3 + 0,5×2 = x(x2 + 1,5)
⇔ x3 – 3×2 + 3x – 1 + 0,5×2 = x3 + 1,5x
⇔ 2,5×2 – 1,5x + 1 = 0
⇔ 5×2 – 3x + 2 = 0; ∆ = 9 – 40 = -31 < 0
pt vô nghiệm
⇔ 2x(x – 7) – 6 = 3x – 2(x – 4)
⇔ 2×2 – 14x – 6 = 3x – 2x + 8
⇔ 2×2 – 15x – 14 = 0; = 225 + 112 = 337
⇔ 14 = x2 – 9 + x + 3
⇔ x2 + x – 20 = 0, ∆ = 1 + 4 . 20 = 81
√∆ = 9
Vậy pt có hai nghiệm x1 = -5, x2 = 4.
Điều kiện: x -1, x 4
pt tương đương với:
2x(x – 4) = x2 – x + 8 ⇔ 2×2 – 8x – x2 + x – 8 = 0
⇔ x2 – 7x – 8 = 0
Có a – b + c = 1 – (-7) – 8 = 0 nên x1 = -1, x2 = 8
Vì x1 = -1 không thỏa mãn điều kiện của ẩn nên: phương trình có nghiệm là x = 8.
Điều 39. Giải thích bằng cách đưa máy phân tích đến máy phân tích.
a) (3×2 – 7x – 10)[2×2 + (1 – √5)x + √5 – 3] = 0;
b) x3 + 3×2- 2x- 6 = 0;
c) (x2 – 1)(0,6x + 1) = 0,6×2 + x;
d) (x2 + 2x – 5)2 = (x2 – x + 5)2.
Đáp án:a) (3×2 – 7x – 10)[2×2 + (1 – √5)x + √5 – 3] = 0
=>hoặc (3×2 – 7x – 10) = 0 (1)
Hoặc 2×2 + (1 – √5)x + 5 – 3 = 0 (2)
Giải (1): pt a – b + c = 3 + 7 – 10 = 0
Nên
Giải (2): pt có a + b + c = 2 + (1 – √5) + 5 – 3 = 0
Nên
b) x3 + 3×2- 2x – 6 = 0 ⇔ x2(x + 3) – 2(x + 3) = 0 ⇔ (x + 3)(x2 – 2) = 0
=>hoặc x + 3 = 0
Hoặc x2 – 2 = 0
Giải ra x1 = -3, x2 = -√2, x3 = 2
c) (x2 – 1)(0,6x + 1) = 0,6×2 + x ⇔ (0,6x + 1)(x2 – x – 1) = 0
=>hoặc 0,6x + 1 = 0 (1)
Hoặc x2 – x – 1 = 0 (2)
(1) 0,6x + 1 = 0
(2): ∆ = (-1)2 – 4 . đầu tiên. (-1) = 1 + 4 = 5, = 5
d) (x2 + 2x – 5)2 = (x2 – x + 5)2 ⇔ (x2 + 2x – 5)2 – (x2 – x + 5)2 = 0
⇔ (x2 + 2x – 5 + x2 – x + 5)( x2 + 2x – 5 – x2 + x – 5) = 0
⇔(2×2 + x)(3x – 10) = 0
⇔ x(2x + 1)(3x – 10) = 0
Hoặc x = 0, x = -1/2 , x = 10/3
Vậy chương trình có 3 cách giải:
x1 = 0, x2 = -1/2 , x3 = 10/3
bài 40. Giải phương trình bằng cách đặt ẩn phụ:
a) 3(x2 + x)2 – 2(x2 + x) – 1 = 0;
b) (x2 – 4x + 2)2 + x2 – 4x – 4 = 0;
c) x – x = 5√x + 7;
Giải: a) Cho t = x2 + x, ta có pt 3t2 – 2t – 1 = 0. Giải pt này ta tìm được hai giá trị của t. Thay từng giá trị của t vừa tìm được vào phương trình t = x2 + x, ta được pt với ẩn số x. Giải từng điểm này sẽ tìm được giá trị của x.
hd: a) 3(x2 + x)2 – 2(x2 + x) – 1 = 0. Đặt t = x2 + x, ta có:
3t2 – 2t – 1 = 0; t1 = 1, t2 = -1/3
Với t1 = 1, ta có: x2 + x = 1 hoặc x2 + x – 1 = 0, Δ = 4 + 1 = 5, √Δ = √5
pt vô nghiệm vì ∆ = 9 – 4 . 3. 1 = -3 < 0
Do đó, có hai nghiệm cho một pt đã cho:
b) (x2 – 4x + 2)2 + x2 – 4x – 4 = 0
Cho t = x2 – 4x + 2 ta có pt: t2 + t – 6 = 0
Giải Ta được t1 = 2, t2 = -3.
– Với t1 = 2 ta có: x2 – 4x + 2 = 2 hay x2 – 4x = 0. Suy ra x1=0 và x2=4.
– Với t1 = -3 ta có: x2 – 4x + 2 = -3 hay x2 – 4x + 5 = 0.
pt này vô nghiệm vì ∆ = (-4)2 – 4 . đầu tiên. 5 = 16 – 20 = -4 < 0
Vậy pt đã cho có hai nghiệm là x1 = 0, x2 = 4.
c) x – √x = 5√x + 7 ⇔ x – 6√x – 7 = 0. Điều kiện: x ≥ 0 . Cho t = √x, t ≥ 0
Ta có: t2 – 6t – 7 = 0. Suy luận: t1 = -1 (loại), t2 = 7
Với t = 7, ta có: √x = 7. Suy ra x = 49.
Vậy phương trình đã cho có nghiệm là: x = 49
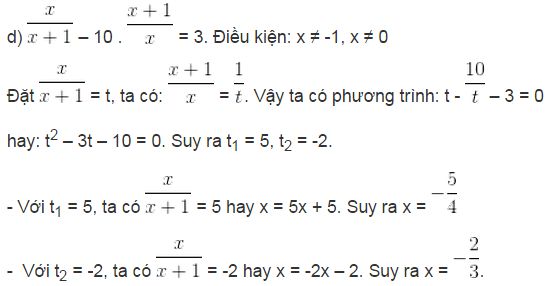
Vậy phương trình đã cho có hai nghiệm là x1 = -5/4 , x2 = -2/3
