Bài 46 Trang 84 – SGK Toán 8 Tập 2
Trong Hình 50, các tam giác đồng dạng được hiển thị. Viết các tam giác này theo thứ tự các đỉnh của chúng và giải thích tại sao chúng bằng nhau?
NGƯỜI CHIẾN THẮNG
Δadc ∽ Δabe vì góc a là chung và \(\widehat{d}\) = \(\widehat{b}\) = 900
Δdef Δbcf vì \(\widehat{d}\) = \(\widehat{b}\) = 900 , \( \widehat{def}\) = ( \widehat{bfc}\)
Δdfe Δbae vì ( \(\widehat{d}\) = \(\widehat{b}\) = 900 , góc chung a)
Δbfc Δdac vì (\(\widehat{d}\) = \(\widehat{b}\) = 900, góc chung c)
Bài 47 Trang 84 – SGK Toán 8 Tập 2
Độ dài các cạnh của tam giác abc là 3cm, 4cm, 5cm. Tam giác a’b’c’ đồng dạng với tam giác abc, có diện tích là 54 cm vuông
Tính khoảng cách đến cạnh a’b’c’ của tam giác.
Người chiến thắng:
Vì abc ∆a’b’c’
=> \( \frac{s_{abc}}{s_{a’b’c’}}\) = \( (\frac{ab}{a’b ‘})^ {2}\)
Các cạnh của abc có độ dài là 3,4,5 nên là tam giác vuông
Suy ra: \( s_{abc}\) = \( \frac{1}{2}\).3.4= 6
Do đó: \( \frac{6}{54}\) = \( (\frac{ab}{a’b’})^{2}\) < = > ; \( (\frac{ab}{a'b'})^{2}\) = \( \frac{1}{9}\)
=> \( \frac{ab}{a’b’}\) = \( \frac{1}{3}\).
=> a’b’ = 3 ab = 3,3
Tức là mỗi cạnh của tam giác a’b’c’ gấp 3 lần cạnh của tam giác abc.
Vậy ba cạnh của tam giác a’b’c lần lượt là 9cm, 12cm, 15cm.
Bài 48 Trang 84 – SGK Toán 8 Tập 2
Bóng của một cây cột điện trên mặt đất dài 4,5m. Đồng thời cắm thẳng đứng một thanh sắt cao 2,1m xuống đất, chiều dài bóng là 0,6m.
Tính chiều cao của cột.
Người chiến thắng:
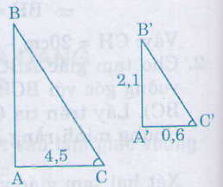
Đồng thời, tia sáng mặt trời chiếu ngang mặt người nên hai tam giác vuông Δabc và Δa’b’c’ đồng dạng.
Δabc ∽ Δa’b’c => \( \frac{ab}{a’b’}\) = \( \frac{ac}{a’c ‘}\)
=> ab = \( \frac{ac.a’b’}{a’c’}\)
=> ab = \( \frac{4,5.2,1}{0,6}\) = 15,75 m
Bài 49 Trang 84 – SGK Toán 8 Tập 2
Trong hình 51, đường cao của tam giác abc vuông góc với a là ah
a) Hình vẽ bên có bao nhiêu cặp tam giác đồng dạng?
b) có nghĩa là: ab = 12,45 cm, ac = 20,50 cm. Tính độ dài các đoạn bc, ah, bh, ch.
Người chiến thắng:
a) ∆abc ∽ ∆hba vì \( \widehat{a}\) = \( \widehat{h}\) = 900 ,\( \widehat{b}\ ) chung
Δabc ∽ hac do \( \widehat{a}\) = \( \widehat{h}\) = 900, \( \widehat{c}\) chung
b) ∆abc là hình vuông tại a =>; bc2 = ab2 + ac2
=> bc2 = 12,452 + 20,502 = 575,2525
=>BC=575,2525 24 cm
ABC
=> \( \frac{ab}{hb}\) = \( \frac{bc}{ba}\) => hb = \( \frac{ab^{ 2}}{bc}\) ≈ \( \frac{12,45^{2}}{24}\) ≈ 6,5 cm
=> ch = bc – bh = 24 – 6,5 ≈ 17,5 cm.
Mặt khác: \( \frac{ac}{ah}\) = \( \frac{ab.ac}{bc}\) = \( \frac{12,45.20 , 25}{24}\)
=>à = 10,6 cm
Bài 50 Trang 84 – SGK Toán 8 Tập 2
Chiều dài bóng của ống khói nhà máy trên mặt đất là 36,9m. Cùng lúc đó, một thanh sắt cao 2,1 mét được cắm thẳng đứng xuống đất và có một quả cầu dài 1,62 mét. Tính chiều cao của ống khói.
Người chiến thắng:
Tương tự bài 48.
abc a’b’c’
\( \frac{ab}{a’b’}\) = \( \frac{ac}{a’c’}\) => \( ab = \frac{a’b’.ac}{a’c’}\)
=> \( ab= \frac{36,9.2,1}{1.62}\)
=>cao 47,8m
Bài 51 Trang 84 – SGK Toán 8 Tập 2
Chân tam giác vuông abc và chiều cao ah chia cạnh huyền bc thành hai đoạn có độ dài 25cm và 36cm. Tính chu vi và diện tích tam giác vuông đó (h.53)
Hướng dẫn: đầu tiên tìm đường đi ah từ các tam giác vuông đồng dạng, sau đó tính các cạnh của tam giác abc.
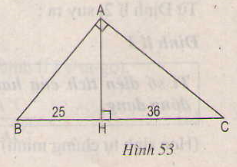
Người chiến thắng:
Δahb ∽ Δcha vì \(\widehat{ahb} = \widehat{ahc}\) = 900,
\(\widehat{bah} = \widehat{ach}\)
\(\frac{ah}{ch}=\frac{bh}{ch}\) => ah2 = ch.bh = 25,36
=>ah2=900=>ah=300
Vậy \(s_{abc}\) = \(\frac{1}{2}\) ah.bc = \(\frac{1}{2}\). 30.(25 + 26) = 915 cm vuông
bài 52 trang 85 – SGK Toán 8 Tập 2
Cho tam giác vuông có cạnh huyền dài 20 cm, cạnh góc vuông dài 12 cm. Tính độ dài hình chiếu của góc vuông còn lại trên cạnh huyền.
Người chiến thắng:
Δabc vuông a có chiều cao ah, bc = 20cm, ab = 12cm. Ta tính hc, abc ∆cba vì
Góc chung b, \( \widehat{a}\) = \( \widehat{h}\) = 900
=> \(\frac{ah}{cb}= \frac{bh}{ba}\) => ab2 = hb.cb
=> bh = \(\frac{ab^{2}}{cb}= \frac{12^{2}}{20}\) = 7,2 (cm)
=>ch = bc – bh = 20 – 7,2 = 12,8
giaibaitap.me
