bài 49 trang 101 sgk toán 7 – tập 1
Hãy chỉ ra giả thiết và kết luận của các định lý sau:
a) Hai đường thẳng song song nếu một đường thẳng cắt chúng sao cho các cặp góc trong xen kẽ bằng nhau.
b) Nếu một đường thẳng cắt hai đường thẳng song song thì hai góc trong bằng nhau.
NGƯỜI CHIẾN THẮNG
a) Giả sử: Một đường thẳng cắt hai đường thẳng sao cho có một cặp góc kề trong thì bằng nhau. Kết luận: Hai đường thẳng song song.
b) Giả sử: Một đường thẳng cắt hai đường thẳng song song. Kết luận: Hai góc trong xen giữa thì bằng nhau.
loigiaihay.com
Đã đăng 50 trang 101 SGK Toán 7 – Tập 1
a) Viết kết luận của định lý sau bằng cách điền vào chỗ trống (…): Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì …
b) Vẽ phát biểu của các định lý và viết các giả thiết và kết luận bằng các ký hiệu.
Hướng dẫn giải quyết:
a) Hai đường thẳng khác nhau song song với nhau nếu chúng cùng vuông góc với đường thẳng thứ ba.
hai)
.
Bài 51 Trang 101 – SGK Toán 7
a) Viết định lí về đường thẳng vuông góc với một trong hai đường thẳng song song.
b) Vẽ sơ đồ và dùng ký hiệu để ghi giả thiết và kết luận.
Người chiến thắng:
a) Nếu một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia.
b) Nhìn vào bức tranh.
Giả định, kết luận:
Sau 52 trang 101 – SGK Toán 7
Xem hình 36, điền vào chỗ trống (…) để chứng minh định lí: “Hai góc đối đỉnh thì bằng nhau”.
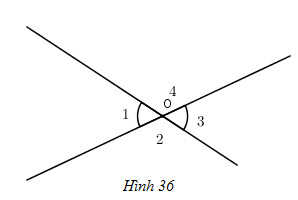
gt: …
kl: …
Định lý
Lý do khẳng định
1
\(\widehat{o_{1}}\) + \(\widehat{o_{2}}=180^0\)
Bởi vì…
2
\(\widehat{o_{3}}\) + \(\widehat{o_{2}}\) = …
Bởi vì…
3
\(\widehat{o_{1}}\) + \(\widehat{o_{2}}\) = \(\widehat{o_{3}}\) + \(\widehat{o_{2}}\)
Dựa trên…
4
\(\widehat{o_{1}}\) = \(\widehat{o_{3}}\)
Dựa trên…
Bằng chứng tương tự \(\widehat{o_{2}}\) = \(\widehat{o_{4}}\)
Người chiến thắng:
Giả định: \(\widehat{o_{1}}\) đỉnh tương đối \(\widehat{o_{3}}\).
Kết luận: \(\widehat{o_{1}}\) = \(\widehat{o_{3}}\)
Định lý
Lý do khẳng định
1
\(\widehat{o_{1}}\) + \(\widehat{o_{2}}=180^0\)
Vì \(\widehat{o_{1}}\) và \(\widehat{o_{2}}\) liền kề
2
\(\widehat{o_{3}}\) + \(\widehat{o_{2}}=180^0\)
Vì \(\widehat{o_{2}}\) và \(\widehat{o_{2}}\) liền kề
3
\(\widehat{o_{1}}\) + \(\widehat{o_{2}}\) = \(\widehat{o_{3}}\) + \(\widehat{o_{2}}\)
Dựa trên 1 và 2
4
\(\widehat{o_{1}}\) = \(\widehat{o_{3}}\)
Dựa trên 3
Chứng minh rằng \(\widehat{o_{2}}\) = \(\widehat{o_{4}}\)
Định lý
Lý do khẳng định
1
\(\widehat{o_{1}}\) + \(\widehat{o_{2}}=180^0\)
Vì \(\widehat{o_{1}}\) và \(\widehat{o_{2}}\) liền kề
2
\(\widehat{o_{1}}\) + \(\widehat{o_{4}}=180^0\)
Vì \(\widehat{o_{1}}\) và \(\widehat{o_{4}}\) liền kề
3
\(\widehat{o_{1}}\) + \(\widehat{o_{2}}\) = \(\widehat{o_{1}}\) + \(\widehat{o_{4}}\)
Dựa trên 1 và 2
4
\(\widehat{o_{2}}\) = \(\widehat{o_{4}}\)
Dựa trên 3
Bài 53 Trang 102 SGK Toán 7 – Tập 1
Cho định lý: “Nếu hai đường thẳng xx’, yy’ cắt nhau tại o và góc quay là góc vuông thì các góc yox’, x’oy’, y’ox lần lượt là một góc vuông”.
a) Vẽ hình. b) Viết các giả thiết và kết luận của định lý. c) Điền các giả thiết và kết luận của định lý. 1) \(\widehat{xy}+\widehat{x) ‘oy}=180^{\circ}\) (vì…). 2) \(90^{\circ}+\widehat{x’oy}=180^{\ circ}\) (giả định và dựa trên…). 3) \(\widehat{x’oy}=90^{\circ}\) (dựa trên …). 4) \(\widehat{x’oy’}=\widehat{rotation}\) (vì…). 5) \(\widehat{x’oy’}=90^{\circ}\) (dựa trên …). 6) \(\widehat{y’ox}=\widehat{x’oy}\) (vì…). 7) \(\widehat{y’ox}=90^{\circ}\) (dựa trên …).d) trình bày lại chứng minh ngắn gọn hơn.
Hướng dẫn giải:a) Xem hình ảnh.
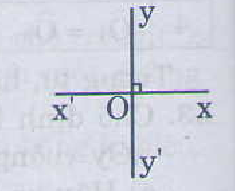b)
c) Điền vào chỗ trống: 1) \(\widehat{spin}+\widehat{x’oy}=180^{\circ}\) (vì là hai góc ) kề ).2) \(90^{\circ}+\widehat{x’oy}=180^{\circ}\) (giả định và dựa trên 1 ).3) \(\widehat{x’oy}=90^{\circ}\) (dựa trên 2).4) \( widehat{x ‘oy’}=\widehat{spin}\) (vì là hai góc đối đỉnh). 5) \(\widehat{x) ‘oy ‘}=90^{\circ}\) (dựa trên 4 và giả định). 6) \(\widehat{y’ox}= widehat{x’ oy}\) (vì là hai góc đối đỉnh). 7) \(\widehat{y’ox}=90^{\circ} ) (dựa trên 6 và 3).d) trình bày lại chứng minh theo cách cô đọng hơn . Ta có: \(\widehat{xy}+\widehat{x ‘oy}=180^{\circ }\) (hai góc kề bù nhau) \(\widehat{xoay }=90 ^{\circ}\) (gt) nên \(90^ {\circ}+\widehat{ x’oy}=180^{\circ}\).suy ra ( widehat{x’oy}=90^{\circ} ) có \(\widehat{x ‘oy’}=\widehat{rotate}\) (hai góc đối đỉnh) . Vậy \(\widehat{y’ox}= 90^{\circ}\).
giaibaitap.me
