Trong chương trình toán THCS khối đa diện chiếm một lượng lớn kiến thức nên hôm nay Thầy Kiến sẽ chia sẻ với các em bộ công thức hình học 12 về khối đa diện.
Tôi hy vọng rằng thông qua bài viết này, bạn có thể có được một tài liệu đánh giá ngắn gọn, chính xác và có thể áp dụng được. Bài viết chỉ nhắc lại một số định nghĩa cơ bản, đồng thời tổng hợp một sốcông thức tính nhanh thể tích 12. Vui lòng đọc kỹ:
Tôi. Một số khái niệm cần nhớ về công thức hình học 12 khối đa diện.
1. Ý tưởng.
Khối đa diện: là hình được tạo bởi một số hữu hạn thỏa mãn hai tính chất:
+ Hai đa giác phân biệt có thể có hoặc không có điểm chung, hoặc chỉ có một đỉnh chung, hoặc chỉ có một cạnh chung.
+ Mỗi cạnh của một đa giác bất kỳ là cạnh chung của đúng 2 đa giác.
Khối đa diện: là không gian được bao bởi một khối đa diện, kể cả khối đa diện đó.
Khối đa diện giới hạn bởi một lăng trụ gọi là lăng trụ đứng. Cũng như vậy, nếu nó bị giới hạn bởi hình chóp thì gọi là khối chóp,…
Trong tin học, chúng ta thường nói đến khối đa diện lồi: tức là khối đa diện (h) thỏa mãn điều kiện là nếu nối 2 điểm bất kỳ của (h) thì ta được một đoạn thẳng thuộc (h).
Đối với một đa diện lồi, mối quan hệ giữa số đỉnh d, số cạnh c và số mặt m có công thức Euler: d-c+m=2.
Khối đa diện đều là khối đa diện lồi có các tính chất sau:
+ Mỗi mặt của nó là đa giác đều p cạnh.
+ Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
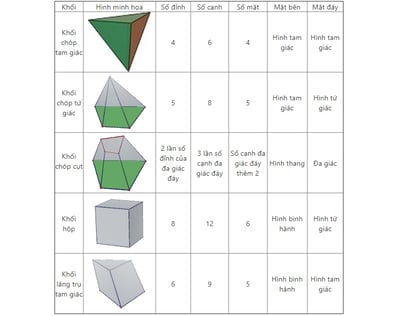
Một số khối đa diện lồi thông dụng:
Ví dụ về khối đa diện:
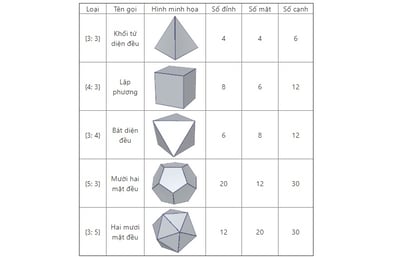
Ví dụ về khối không đa diện:
2. Phân vùng và lắp ghép các khối đa diện.
Những điểm không thuộc khối đa diện được gọi là điểm nằm ngoài, tập hợp các điểm nằm ngoài được gọi là trường nằm ngoài. Các điểm thuộc khối đa diện nhưng không thuộc khối đa diện ngoài được gọi là các điểm trong khối đa diện và tương tự, tập hợp các điểm bên trong tạo nên miền bên trong của khối đa diện.
Cho khối đa diện (h) là hợp của hai khối đa diện (h1) và (h2), (h1) và (h2) không có điểm chung thì ta nói (h) có thể chia thành hai phần (h1 ) và (h2), trong khi người ta có thể nói rằng việc kết hợp hai khối (h1) và (h2) sẽ tạo ra khối (h).
Ví dụ: Cắt lăng trụ abc.a’b’c’ bằng mặt phẳng (a’bc) ta được hai khối đa diện mới a’abc và a’bcc’b’ .
3. Một số kết quả quan trọng.
kq1: Cho tứ diện đều:
+ Trọng tâm của mặt là đỉnh của tứ diện đều.
+Trung điểm các cạnh là đỉnh của khối bát diện đều.
kq2: Đối với hình lập phương, tâm các mặt của nó sẽ tạo thành một bát diện đều.
kq3: Đối với một bát diện đều, tâm của các mặt của nó sẽ tạo thành một hình lập phương.
kq4: Hai đỉnh của một khối bát diện đều được gọi là cặp đỉnh nếu chúng không thuộc cùng một mặt của hình lập phương. Đoạn thẳng nối hai đỉnh đối diện gọi là đường chéo của một bát diện đều. Sau đó:
+ Ba đường chéo cắt nhau tại trung điểm của mỗi đường.
+ Ba đường chéo đôi một vuông góc với nhau.
+ Ba đường chéo bằng nhau.
kq5: Một hình đa diện phải có ít nhất 4 mặt.
kq6: Khối đa diện có ít nhất 6 cạnh.
kq7: Không có hình đa diện nào có 7 cạnh.
Làm quen với hình học và cách đạt điểm 8+ môn toán một cách dễ dàng. Nhấp vào đây để tìm hiểu thêm về khóa học này: Tap 8+ Toán 12. Bạn sẽ được kèm cặp bởi một giáo viên với hơn 9 năm kinh nghiệm giảng dạy và luyện thi đại học. Hơn 400.000 lượt theo dõi trên các kênh facebook, tiktok, youtube. Đặc biệt, hãy đăng ký ngay hôm nay và Ant House dành tặng bạn 50% học phí!
Hai. Tổng hợp công thức hình học về khối đa diện 12 khối.
1. Thể tích kim tự tháp:
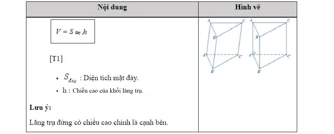
2. Thể tích lăng trụ:
3. Thể tích hình khối:
Lưu ý: Hình lập phương là hình chữ nhật có các cạnh dài bằng nhau.
4. Công thức tỷ lệ thể tích
Lưu ý đặc biệt: Công thức tỉ số thể tích chỉ áp dụng cho hình chóp tam giác. Nếu gặp hình chóp tứ giác, ta cần chia thành 2 hình chóp tam giác để áp dụng công thức này.
5. Công thức tính nhanh 12 dòng riêng:
Đường chéo của hình lập phương cạnh a có độ dài: 
SS
Cho hình hộp có độ dài 3 cạnh là a, b, c thì độ dài đường chéo là: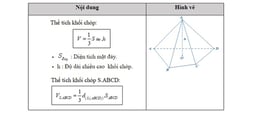 
Đường cao của tam giác đều cạnh a là: 
Ngoài ra, để tính thể tích khối đa diện, bạn cần nhớ một số công thức toán phẳng:
Cho tam giác vuông abc tại a, xét chiều cao ah. Sau đó:
Công thức tính diện tích tam giác abc có độ dài 3 cạnh là a, b, c; các chiều cao tương ứng là ha, hb, hc; bán kính đường tròn ngoại tiếp là r; bán kính đường tròn nội tiếp hình tròn là r; nửa chu vi của tam giác là
Trên đây là phần tổng hợp các bài giải chuyên đề thể tích khối đa diện Dạng toán 12 bằng kiến. Mong rằng qua bài viết này các bạn sẽ ôn tập và nâng cao kiến thức của mình. Mọi dạng toán đều cần sự tỉ mỉ cẩn thận, vì vậy ghi nhớ các công thức một cách chính xác cũng là một cách để cải thiện điểm số của bạn trong mỗi bài kiểm tra. Ngoài ra, bạn cũng có thể tham khảo thêm các bài viết khác của kiến để biết thêm nhiều điều bổ ích. chúc may mắn.
