Dịch Công thức – Toán lớp 11
1. Lý thuyết
Trong mặt phẳng của vectơ. Phép biến hình biến mỗi điểm m thành điểm m’ sao cho mm’→=v→ được gọi là phép tịnh tiến theo véc tơ v→.
Phép tịnh tiến dọc theo vectơ v→ thường được biểu thị là tv→, và v→ được gọi là vectơ tịnh tiến.
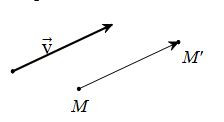
Vậy, tv→m=m’⇔mm’→=v→.
Dịch chuyển theo vectơ – không được gọi là đồng nhất hóa. (Tự đưa ra từng điểm)
* thuộc tính
– Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kỳ.
– Làm cho một đường thẳng song song hoặc trùng với nó.
– Sử dụng công cụ này để biến một vectơ thành một vectơ.
– Sử dụng công cụ này để biến hình tam giác thành hình tam giác.
– Biến góc thành góc đều.
– Biến hình tròn thành hình tròn có cùng bán kính.
2. công thức
Trong mặt phẳng tọa độ Oxy của vectơ v→=a;b. Với mỗi điểm m(x;y) ta có m'(x’;y’) là ảnh của m tịnh tiến dọc theo v→. Khi đó mm’→=v→⇔x’=x+ay’=y+b.
(Tọa độ ảnh=tọa độ điểm+tọa độ vectơ tịnh tiến)
3. Ví dụ
Ví dụ 1: Trong mặt phẳng tọa độ Oxy của vectơ v→=(1;−5), điểm a(2; 2), đường thẳng d: 3x + 4y – 4 = 0, đường tròn : (c): x2 + y2 – 2x + 4y – 1 = 0 . định nghĩa:
a) Điểm a’ là ảnh của a qua phép tịnh tiến theo vectơ v→.
b) Đường thẳng d’ là ảnh của d sau phép tịnh tiến theo véc tơ v→.
c) Đường tròn (c’) là ảnh của (c) sau phép tịnh tiến theo véc tơ v→.
Giải pháp
a) Ta có a’, là hình ảnh qua tv→. Tọa độ a’: xa’=xa+1=3ya’=ya−5=−3. Vậy a'(3; -3).
b) Lấy điểm m(0; 1) thuộc d
Qua tv → gọi m’ là ảnh của m thì m’∈d’
Ta có: xm’=xm+1=1ym’=ym−5=−4. Vậy m'(1;-4) .
Vì d’ là ảnh của d qua tv→ nên d’ song song hoặc trùng với d. Đạo hàm vtpt nd’→=nd→=3;4.
Vậy phương trình d’: 3(x – 1) + 4(y + 4) = 0. hay d’: 3x + 4y + 13 = 0.
c) Cách 1: (tâm thuần i, giữ nguyên bán kính)
Phương trình đường tròn (c): x2 + y2 – 2x + 4y – 1 = 0
Tâm tại i (1; -2) và bán kính r=12+−22−−1=6
Qua TV → Hãy gọi tôi là hình ảnh của tôi. Ta có: xi’=xi+1=1+1=2yi’=yi−5=−2−5=−7.
Tôi'(1; -7)
Đường tròn (c’) là hình của (c) đến , nên (c’) có tâm i’ và bán kính .
Vậy phương trình (c’): (x-2)2 + (y+7)2 = 6 hoặc x2 + y2 – 4x + 7y + 47 = 0.
Cách 2: (biến đổi từng điểm trên đường tròn)
Với mọi điểm b(x;y) ∈(c). Gọi b'(x’;y’) là ảnh tịnh tiến của b.
Sau đó x’=x+1y’=y−5⇔x=x’−1y=y’+5
Vì bx;y∈c nên thay vào phương trình (c):
(x’- 1)2 + (y’ + 5)2 – 2(x’ – 1) + 4(y’+ 5) – 1 = 0
Suy ra x’2 + y’2 – 4x’ + 14y’ + 47 = 0
b'(x’;y’) b qua ảnh của tv → nên b’ di chuyển trên đường tròn (c’): x’2 + y’2 – 4x’ + 14y’ + 47 = 0
Vậy ảnh của (c) là đường tròn (c’): x’2 + y’2 – 4x’ + 14y’ + 47 = 0
Ví dụ 2: Cho hai parabol (p): y = x2 và (q): y = x2 + 2x + 2 trên mặt phẳng với hệ tọa độ Oxy. Tìm phép tịnh tiến để biến ( q ) thành (p).
Giải pháp
Gọi vectơ tịnh tiến là v→=a;b. Cho ảnh của (q) qua tv → gọi là parabol (r)
Lấy mx;y∈(q). Gọi m’x’;y’=tv→(m) thì m’∈r
Biểu thức tọa độ để áp dụng bản dịch: x’=x+ay’=y+b⇔x=x’−ay=y’−b
Vì , thế vào phương trình (q): y’ – b = (x’ – a)2 + 2(x’- a) + 2
⇔y’=x’2+ 21-ax’+a2-2a+b+2
Vậy phương trình (r): y = x2 + 2(1 – a)x + a2 – 2a + b + 2
Nếu (r) trùng với (p) thì 2(1−a)=0a2−2a+b+2=0
⇔a=112−2.1+b+2=0⇔a=1b=−1
Vậy theo vectơ v→−1;1 chỉ có một phép tịnh tiến biến parabol (q) thành parabol (p).
4. Tự luyện tập
câu 1. Trên mặt phẳng tọa độ Oxy, cho phân số m(0; 1). Điểm m qua u→1;2 phép tịnh tiến theo véc tơ như thế nào?
a. m'(2; 3)
b. m'(1; 3)
c. m'(1; 1)
d. m'(-1; -1)
Câu 2. Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x – 2y + 2 = 0. Hình dịch chuyển bởi đường thẳng d qua u→=2;3 có phương trình:
a. x + 2y + 2 = 0
b. x – 2y + 6 = 0
c. 2x – y + 2 = 0
d.2x + y +2 = 0
Câu 3. Trong mặt phẳng tọa độ Oxy, cho đường tròn (c): x2 + y2 – 2x + 4y – 4 = 0. Đường tròn (c) tịnh tiến ảnh của u→1 theo vectơ; 1 là một đường tròn có phương trình:
a. (x – 2)2 + (y + 1)2 = 16
b. (x + 2)2 + (y – 1)2 = 9
c. (x – 2)2 + (y + 1)2 = 9
d. (x + 2)2 + (y + 1)2 = 9
Đáp án:1b, 2b, 3c
Xem tổng hợp công thức toán lớp 9 đầy đủ và chi tiết hơn:
Công thức đối xứng
Công thức đối xứng trục
công thức xoay
Công thức vị ngữ
Công thức đồng dạng
