Phân viên – công thức tính diện tích chính xác nhất
Học sinh chắc chắn đã quen với khái niệm phân viên, nhưng mới chỉ ở mức độ cơ bản với loài kiến. Tuy nhiên, bạn có chắc chắn về công thức diện tích và các ứng dụng của nó. Vì vậy, nếu bạn thắc mắc về cách tính diện tích hình lập phương, bài viết này sẽ là một lựa chọn hợp lý để bạn tìm ra lời giải!
I. Định nghĩa
Hình elip là hình tròn giới hạn bởi các cung và các đường căng của chúng.
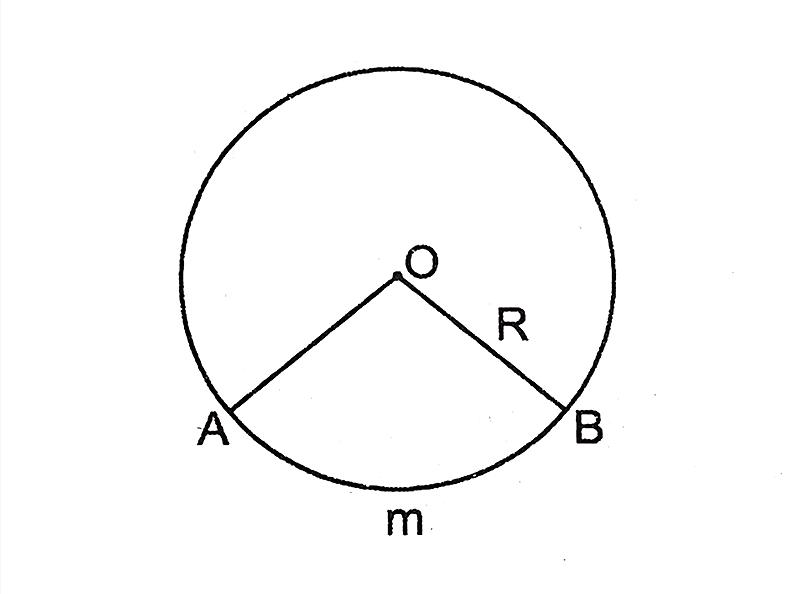
Vị trí:
- Độ dài của hợp âm ab là m
- r là bán kính đường tròn giới hạn
- Diện tích bao bởi cung tròn và tâm của đường tròn là:
- Chia cả hai vế cho \({\displaystyle {\pi r^{2}}}\)
- Tỷ số diện tích a với diện tích giới hạn của hình tròn bằng tỷ số độ lớn của góc \({\displaystyle \theta}\) với độ lớn của cả hình tròn :
- Đơn giản hóa \({\displaystyle \pi }\) trên cả hai bên
- Nhân cả hai vế với \({\displaystyle r^{2}}\) để được
- Tương tự như trên, nếu góc tính bằng độ thì công thức tương đương:
- Nắm chắc các nguyên tắc cơ bản
- Thực hành các bài toán về công thức diện tích hình hộp chữ nhật trong sách giáo khoa hoặc sách tham khảo của bạn.
- Tham gia thảo luận trên lớp, làm bài tập nhóm và hỏi ý kiến của giáo viên là một cách học hay mà nhiều sinh viên sử dụng.
- Tìm thêm các bài giảng và bài tập trên các trang mạng xã hội liên quan đến học tập như Cùng học,…
- Công thức tính diện tích quả bóng nhỏ
Hai. Công thức tính diện tích phân
1. Việc tính diện tích của quả bóng phân được thể hiện theo công thức sau
\({\displaystyle {\dfrac {1}{2}}r^{2}(\theta -\sin {\theta })}\)
Tính diện tích của hình elip bằng cách lấy dây cung trừ đi hai bán kính.
Xem thêm:Công thức tính diện tích hình lập phương
2. Công thức tính diện tích hình tròn hữu hạn:
\({\displaystyle a={\dfrac {1}{2}}r^{2}\theta .}\)
\({\displaystyle {\dfrac {a}{\pi r^{2}}}={\dfrac {\theta }{2\pi }}.}\)
\({\displaystyle {\dfrac {a}{r^{2}}}={\dfrac {\theta }{2}}.}\)
\({\displaystyle a={\dfrac {1}{2}}r^{2}\theta .}\)
\({\displaystyle a={\dfrac {\alpha }{360}}\pi r^{2}.}\)
Ba. Thực hành
Phần 1: Quả bóng phân là một hình tròn giới hạn bởi một đường cung và lực căng của nó. Tính diện tích hình lập phương biết góc giữa tâm aob = 60 độ và bán kính hình tròn là 5,1cm?
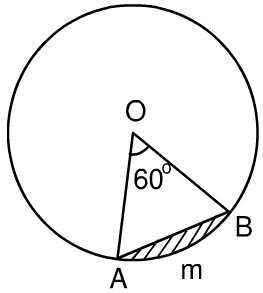
Giải pháp thay thế:
Ta có s quả bóng phân = s cung aob – s tam giác aob
s fan aob = \(\dfrac{\pi.r^2.n}{360 ^{\circ}}= \dfrac{\pi.5.1^2.60^{ circ }}{360 ^{\circ}}= 13,61(cm^2)\)
s tam giác aob = \(\dfrac{r^2\sqrt3}{4}= \dfrac{5,1^2\sqrt3}{4}= 11,26 (cm^2 )\ )
\(svp= 13.61-11.26= 2.35(cm^2)\)Câu 2: Cho dãy bàn bc = a cung \( bc=90^0\) .Tính diện tích hình lập phương.
Giải pháp thay thế:
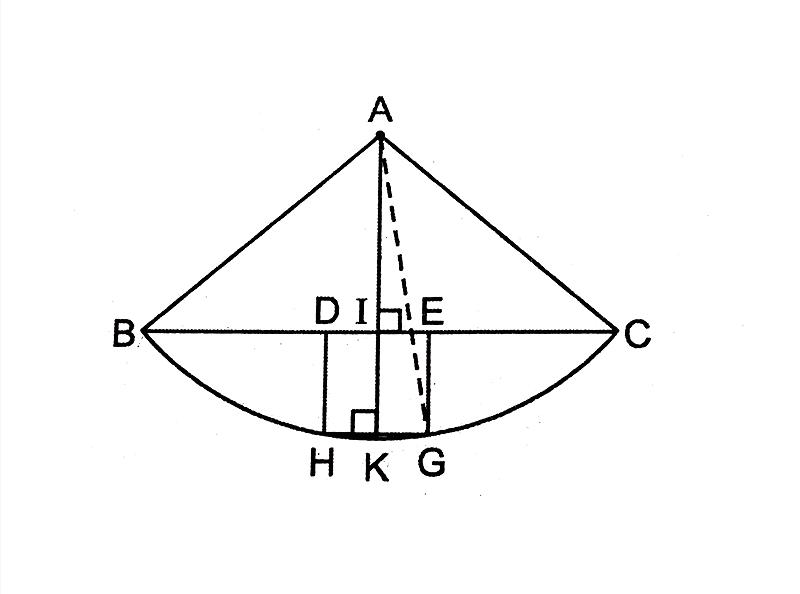
Cho a là tâm của cung bc. Ta có bc = a nên:
\(ac=\dfrac{a}{\sqrt2}\).Ta có thể tính diện tích hình lập phương bằng cách:
\(s=\dfrac{a^2}{8}(\pi -2)\).
Đọc thêm: bài 85 trang 100 sgk toán 9 tập 2
Dưới đây là một số mẹo để đảm bảo bạn có kiến thức liên quan đến dạng bài tập này:
Chúng tôi hy vọng bài viết về công thức tính diện tích hình lập phương trên đây sẽ là sự lựa chọn tốt nhất và hữu ích cho bạn đọc trong quá trình ôn tập. Chúng tôi luôn mong muốn cung cấp những thông tin cần thiết nhất một cách ngắn gọn và súc tích nhất để bạn có thể dễ dàng hiểu được. Mọi ý kiến đóng góp có thể để lại ở phần bình luận, chúng tôi sẽ cố gắng khắc phục và hoàn thiện hơn. Cám ơn vì sự quan tâm của bạn!
