1. Định nghĩa
Michael Faraday, người đã đưa ra khái niệm điện trường vào thế kỷ 19, đề xuất rằng không gian xung quanh một vật tích điện chứa đầy các đường sức. Mặc dù chúng ta không còn coi các đường lực là một thực thể, nhưng các đường lực vẫn đóng vai trò là một cách trực quan rất tốt để mô tả điện trường.
Mối quan hệ giữa đường sức và vectơ điện trường như sau: (1) Tại bất kỳ điểm nào, hướng của đường sức hoặc hướng tiếp tuyến của đường cong đều cho ( \overrightarrow{e}\ ) tại điểm đó và (2) vẽ đường sức sao cho số đường sức của mỗi điện tích đồng vị nằm trong mặt phẳng vuông góc với các đường sức tỉ lệ với độ lớn của các đường sức \( \overrightarrow{e} \). Cái sau có nghĩa là e lớn khi các đường sức ở gần và e nhỏ khi các đường sức thưa thớt.
Đường sức điện trường hay đường sức là đường mà tiếp tuyến của mỗi điểm trùng với phương của véc tơ cường độ điện trường tại điểm đó và phương của đường sức là phương của cường độ điện trường và véc tơ cường độ điện trường.
p>
Tập hợp các đường sức điện trường này được gọi là quang phổ điện trường. Phổ điện mô tả trực quan sự phân bố điện trường.
2. Thuộc tính
Có thể vẽ một đường sức qua bất kỳ điểm nào trong + điện trường. Thật vậy, cường độ điện trường \( \overrightarrow{e} \) tại một điểm bất kỳ trong điện trường đều có giá trị xác định nên ta có thể vẽ đường sức qua điểm đó.
+ Các đường sức không cắt nhau. Vì nếu chúng cắt nhau thì sẽ có hai vectơ cường độ điện trường tại giao điểm – điều này là vô lý.
+ Các đường sức của trường tĩnh điện không khép kín, đi (xuất phát) từ điện tích dương và đi vào (kết thúc) điện tích âm.
+ Đường sức điện trường đều là những đường sức song song cách đều nhau. Thật vậy, vì vectơ \( \overrightarrow{e} \) giống nhau tại mọi điểm nên theo tính chất 1 và 2, các đường sức phải song song và cùng chiều. Do giá trị \( e = const\) của mọi điểm nên mật độ của các đường sức là như nhau tại mọi điểm theo quy ước 3, nghĩa là các đường sức cách đều nhau.
3. Quy ước vẽ
Vẽ số đường sức điện đi qua đồng vị có diện tích bề mặt \( \delta s\) (đủ nhỏ), vuông góc với đường sức bằng độ lớn của vectơ cường độ điện trường. (Như trong Hình 1.18)
Suy luận, nơi điện trường mạnh thì đường sức dày, nơi điện trường yếu thì đường sức mảnh, nơi điện trường đều thì các đường sức song song và cách đều nhau.
Số đường sức vuông góc với đường sức đi qua một đơn vị diện tích gọi là mật độ điện trường. Do đó véc tơ cường độ điện trường tại mỗi điểm bằng mật độ điện trường tại điểm đó.
Hình 1.19 và 1.20 là một số dạng đường sức điện trường. Từ đó ta có thể thấy rằng, ở gần điện tích thì điện trường rất mạnh.
a) Đường sức điện trường của điện tích điểm dương.
b) Đường sức điện trường của điện tích điểm âm.
c) Đường sức của điện trường đều.
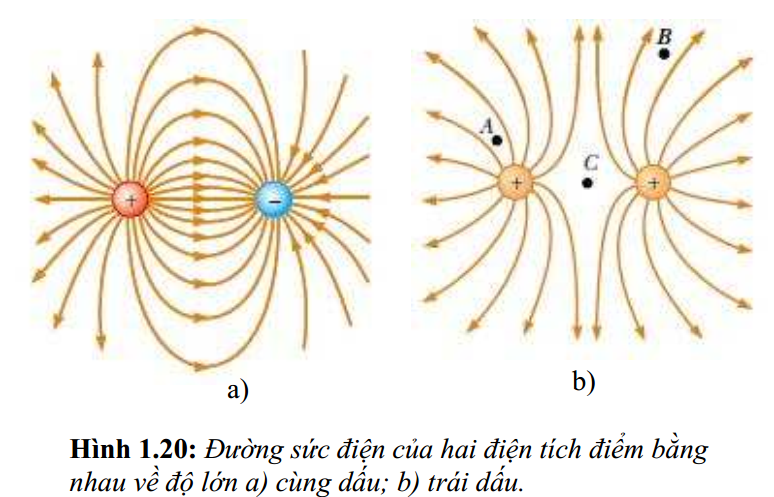
Theo sự phân bố các đường sức tại a, b, c trên hình b) suy ra được cường độ điện trường ea >;eb >Thương mại điện tử
