Định nghĩa, phân loại và đặc điểm của sóng cơ học. Phương trình sóng cơ học phụ thuộc vào thời gian và không gian được trình bày rất chi tiết.
Sóng cơ học và sự truyền
a.Lý thuyết
1. Định nghĩa-phân loại sóng cơ học
+ Sóng cơ học là những dao động lan truyền trong một môi trường.
+ Khi sóng cơ lan truyền thì chỉ có pha dao động của các phần tử vật chất lan truyền, còn các phần tử vật chất dao động quanh một vị trí cân bằng cố định.
+ Sóng biến dạng là sóng trong đó phương dao động của hạt môi trường vuông góc với phương truyền sóng. Ví dụ, sóng trên mặt nước, sóng trên dây cao su.
+Sóng dọc là sóng trong đó phương dao động của phần tử môi trường trùng với phương truyền sóng.
Ví dụ: sóng âm, sóng mùa xuân.
2. Đặc điểm của sóng hình sin
+Biên độ sóng a: là biên độ dao động của phần tử môi trường mà sóng truyền qua.
+ Chu kì sóng t: là chu kì dao động của phần tử trong môi trường truyền sóng.
+tần số f: là nghịch đảo của chu kỳ sóng: f = \(\frac{1}{t}\)
+ Vận tốc Phương trình truyền sóng v: là vận tốc truyền sóng của dao động trong môi trường. Phụ thuộc vào tính chất của môi trường (\(v_{r}>v_{l}>v_{k}\)) và nhiệt độ (nhiệt độ của môi trường càng cao sẽ làm tăng nhanh hơn tốc độ lan truyền)
+ Bước sóng λ: là quãng đường sóng truyền được trong một chu kỳ. λ = vt = \(\frac{v}{f}\).
+bước sóng λ cũng là khoảng cách giữa hai điểm gần nhau nhất trên cùng một pha truyền sóng.
+Khoảng cách giữa hai điểm gần nhau nhất trên một phương sóng dao động cùng pha là \(\frac{\lambda }{2}\).
+Khoảng cách giữa hai điểm gần nhau nhất trên phương truyền sóng của phương dao động vuông góc là \(\frac{\lambda }{4}\) .
+ Khoảng cách giữa hai điểm bất kỳ trên mặt sóng dao động cùng pha là: kλ.
+Khoảng cách giữa hai điểm bất kì dao động cùng pha trên phương truyền sóng là: (2k+1)\(\frac{\lambda }{2}\).
+Chú ý: Giữa n pic (đỉnh) có (n – 1) bước sóng.
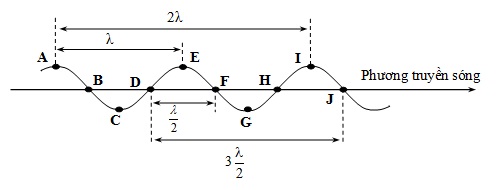
3. Phương trình sóng:
a.at source o: uo =aocos(ωt)
b.at m theo phương truyền sóng:
um=amcosω(t- ∆t)
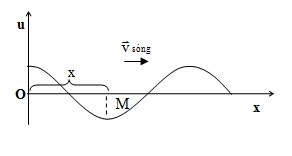
Nếu bỏ qua sự mất mát năng lượng trong quá trình lan truyền thì biên độ tại o và m bằng nhau: ao = am = a.
Sau đó:um =acosω(t – \(\frac{x}{v}\)) =acos 2π(\(\frac{t}{t} -\frac{x}{\lambda }\)) t ≥ x/v
Tổng quát: Tại điểm o: uo = acos(ωt + φ).
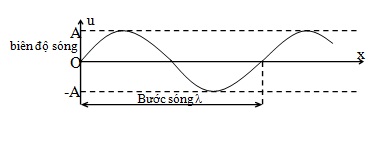
d.at m cách o một khoảng x theo phương truyền sóng.
* Sóng truyền theo chiều dương của trục bò:
um = amcos(ωt + φ – \(\omega \frac{x}{v}\) ) = amcos(ωt + φ – \(2\pi \frac{x} {\lambda }\)) t ≥ x/v
* Sóng truyền theo chiều âm của trục tăng:
um = amcos(ωt + φ + \(\omega \frac{x}{v}\)) = amcos(ωt +φ+ \(2\ pi \frac{x}{\lambda }\))
–Tại một điểm m cho trước trong một môi trường sóng: x = const; um là một hàm điều hòa của t với chu kỳ t.
–Tại thời điểm xác định t= const ; um là hàm biến thiên điều hòa trong không gian x với chu kỳ .
e.Độ lệch pha giữa hai điểm có khoảng cách xm, xn: \(\delta \varphi _{mn}=\omega \frac{ x_{n}-x_{m}}{v}=2 \ pi \frac{x_{n}-x_{m}}{\lambda }\)
+Nếu 2 điểm m và n dao động ngược pha thì:
\(\delta \varphi _{mn}=2k\pi \leftrightarrow 2\pi \frac{x_{n}-x_{m}}{\lambda }=2k pi \leftrightarrow x_{n}-x_{m}=k\lambda (k\in z)\)
+Nếu 2 điểm m và n dao động ngược pha thì:
\(\delta \varphi _{mn}=(2k+1)\pi \leftrightarrow 2\pi \frac{x_{n}-x_{m}}{\lambda }=(2k+1)\pi\)\(\leftrightarrow x_{n}-x_{m}=(2k+1)\frac{\lambda }{2} (k\in z)\)
+Nếu 2 điểm m và n dao động ngược pha thì:
\(\delta \varphi _{mn}=(2k+1)\frac{\pi }{2} \leftrightarrow 2\pi \frac{x_{n}-x_ {m}}{\lambda }=(2k+1)\frac{\pi }{2}\)\(\leftrightarrow x_{n}-x_{m}=(2k+1) \frac{\lambda }{4} (k\in z)\)
-Nếu 2 điểm m và n nằm trên cùng phương truyền sóng và cách nhau một khoảng x:
\(\delta \varphi =\omega \frac{x}{v}=2\pi \frac{x}{\lambda }\)
(nếu 2 điểm m và n cùng sóng và cách nhau khoảng d thì : \(\delta \varphi =\frac{2 pi d }{\lambda }\) )
– vậy 2 điểm m và n trên phương truyền sóng sẽ:
+ Dao động cùng pha khi: d = kλ
+ Dao động lệch pha khi: d = (2k + 1)\(\frac{\lambda }{2}\)
+ Dao động vuông pha khi: d = (2k + 1)\(\frac{\lambda }{4}\)
k = 0, ±1, ±2 …
Lưu ý: Đơn vị của x, x1, x2, d, l, v phải tương ứng với một đối một.
f. Trong hiện tượng sóng truyền trên một sợi dây,dây bị kích thích dao động bởi một nam châm điện có tần số dòng điện f thì tần số dao động của dây là 2f.
b. Ví dụ
Ví dụ1: Một người ngồi trên bãi biển, nhìn thấy 10 ngọn sóng lướt qua trong 36 giây, khoảng cách giữa 2 ngọn sóng là 10m.. tần số sóng. và vận tốc truyền sóng.
A. 0,25 Hz; 2,5m/s 4 Hz; 25 m/s 25 Hz; 2,5m/s d. 4 Hz; 25 cm/s
Giải: Coi tại một điểm có 10 con sóng đi qua ứng với 9 chu kỳ. t = \(\frac{36}{9}\) = 4s. Xác định tần số của dao động. \(f=\frac{1}{t}=\frac{1}{4}=0,25hz\) .tốc độ sóng:\(\lambda =vt\ mũi tên bên phải v= \frac{\lambda}{t}=\frac{10}{4}=2,5(m/s)\).
MộtÁp dụng một
Ví dụ 2: Sóng cơ di chuyển trên những sợi dây đàn hồi rất dài. Phương trình sóng tại một điểm trên sợi dây: u = 4cos(20π t – \(\frac{\pi x}{3}\) )(mm). x: tính bằng mét, t: giây tính bằng mét. Vận tốc truyền sóng trên một sợi dây có một giá trị.
A. 60 mm/s 60 cm/s 60 m/s 30 mm/s
Mô tả giải: Ta có = \(\frac{\pi x}{3}\) (=\frac{2\pi x}{\lambda }\) => λ = 6 m => v = λ.f = 60 m/s (Lưu ý: x tính bằng mét).
Những ứng viên đã trả lờic
Ví dụ 3: Giả sử sóng cơ truyền theo phương của con bò có biên độ không đổi. Tại o dao động có dạng u = acosωt (cm). Khoảng cách từ tâm dao động o tại thời điểm m là \(\frac{1}{3}\) và bước sóng tại thời điểm bằng 0,5 chu kỳ nên biên độ là 5cm². Phương trình nào sau đây thỏa mãn phương trình dao động tại m:
A. \(u_{m}=acos(\omega t-\frac{2\lambda }{3})cm\) b. \(u_{m}=acos(\omega t- frac{\pi \lambda }{3})cm\)
c. \(u_{m}=acos(\omega t-\frac{2\pi }{3})cm\) d. \(u_{m}= acos(\omega t-\frac{\pi }{3})cm\)
Chọn c
Giải thích cách giải: Sóng truyền từ o đến m mất một khoảng thời gian: t = \(\frac{d}{v}=\frac{\ lambda }{ 3v} ) Phương trình dao động tại m có dạng: \(u_{m}=acos\omega (t-\frac{1.\lambda {v.3})\ ) .với v = λ/ t .suy ra : Ta có: \(\frac{\omega }{v}=\frac{2\pi }{t.\frac{\lambda }{ t} }= frac {2\pi }{\lambda }\) Vậy \(u_{m}=acos(\omega t-\frac{2\pi .\lambda } { lambda . 3} )\) hoặc: \(u_{m}=acos(\omega t-\frac{2\pi }{3} )cm \)
c. Thực hành
bài1 : Một người trên biển nhìn vào một chiếc phao và thấy nó lên xuống. Đặt 16 lần trong vòng 30 giây và khoảng cách giữa 5 đỉnh núi liên tiếp là 24m. Vận tốc truyền sóng trên mặt biển là
Một. v = 4,5m/s b. v = 12m/s. c. v = 3m/s d.v = 2,25 m/s
Bài 2: Một sóng cơ truyền dọc theo trục ox có phương trình \(u=5cos(6\pi t-\pi x)\) (cm), trong đó t tính bằng s và x tính bằng m. Tốc độ sóng này là
a. 3 m/s. b. 60 m/s. c. 6 m/s. d. 30 m/s.
<3 Vận tốc truyền sóng là 40cm/s. Viết phương trình sóng tại m khoảng cách o d=50 cm.
a. \(u_{m}=5cos(4\pi t-5\pi )(cm)\) b. \ (u_{m}=5cos(4\pi t-2,5\pi )(cm)\)
c. \(u_{m}=5cos(4\pi t-\pi )(cm)\) d. \( u_{m}=5cos(4\pi t-25\pi )(cm)\)
Bài4: Có một sóng cơ truyền theo phương bò trên một sợi dây dài vô hạn và có phương trình sóng là u = 2cos ( 10πt – πx) (cm) (với t tính bằng s; x tính bằng m). m và n là hai điểm cách nhau 5m cùng phía của o. Đồng thời khi phần tử m đi qua vị trí cân bằng về phía trước thì phần tử n
a. Vật chuyển động tịnh tiến qua vị trí cân bằng. b. Chiều âm đi qua vị trí cân bằng.
c. đang có lợi. d. trên lợi nhuận âm.
bài 5: Cho phương trình sóng: \(u=asin(0.4\pi x+7\pi t+\frac{) pi }{3})\) (m, s). Phương trình này cho biết:
Một. Sóng truyền dọc theo chiều âm của trục x với vận tốc (m/s)
b. Sóng truyền theo chiều dương của trục x với vận tốc (m/s)
c.Sóng truyền dọc theo chiều dương của trục x với tốc độ 17,5(m/s)
d.Sóng truyền dọc theo chiều âm của trục x với tốc độ 17,5(m/s)
Sau6: Một sóng biến dạng truyền trên một sợi dây đàn hồi rất dài với tần số 500hz. Có thể thấy rằng hai điểm a và b cách nhau 200cm trên dây dao động cùng pha, còn hai điểm khác trên dây ab dao động cùng pha với a. Tốc độ sóng trên đường dây:
a. 500cm/s b. 1000m/s c. 500m/s d. 250cm/
Sau 7: Dao động điều hòa lan truyền từ điểm m đến điểm n liên tục với khoảng cách m là 7λ/3(cm). Sóng truyền với biên độ không đổi a. Biết rằng phương trình sóng tại m có dạng um = 3cos2πt (um tính bằng cm và t tính bằng giây). Tại thời điểm t1, vận tốc dao động của phần tử m là 6π(cm/s) và vận tốc dao động của phần tử n là a.3π(cm/s). b. 0,5π (cm/s). c. 4π(cm/s). d. 6π(cm/s).
Sau8: Sóng cơ truyền trên sợi dây với chu kỳ t, biên độ là a. Tại thời điểm t0, khoảng cách các phần tử tại b và c lần lượt là −24 mm và +24 mm, phần tử tại điểm d thuộc bc ở trạng thái cân bằng. Tại thời điểm t1, nếu vật ở b và c cách đều +10mm thì vật ở d cách xa vị trí cân bằng
a.26mm b.28mm c.34mm d.17mm
Bài 9: Một sóng truyền từ nguồn o theo phương thẳng với biên độ không đổi. Tại thời điểm t = 0, điểm o đi qua vị trí cân bằng theo chiều (+). Ở thời điểm tức thời của 1/2 chu kỳ, một điểm cách nguồn 1 khoảng 1/4 bước sóng, ở khoảng cách 5 cm. Biên độ là a.10cm b.5\(\sqrt{3}\)cmc.5 ( sqrt{2}\) cm d. 5cm
Bài 10: Đối với sóng cơ học truyền trên đường thẳng thì phương truyền tại nguồn o là:
uo = acos( \(\frac{2\pi }{t}t+\frac{\pi }{2}\) ) (cm). Tại thời điểm t = 1/2 chu kì, điểm m cách nguồn bằng 1/3 bước sóng, độ dời um = 2(cm). Biên độ a là
a. 4cm. b. 2 cm. c. 4/\(\sqrt{3}\) cm. d. 2\(\sqrt{3}\) cm
Tất cả nội dung bài viết. Vui lòng xem thêm và tải về các tài liệu chi tiết sau:
Tải xuống
Bài tập trắc nghiệm Vật Lý lớp 12 – Xem ngay
