Lý thuyết và phương pháp trung tâm
1. Lệch pha đồng thời 2 điểm
Xét 2 điểm m,n cách nhau ${{x}_{1}},{{x}_{2}}.$
Phương trình sóng tại m là ${{u}_{m}}=a\cos \left( \omega t-\frac{2\pi {{x}_{1}} }{\lambda } \right).$
Phương trình sóng tại n là ${{u}_{n}}=a\cos \left( \omega t-\frac{2\pi {{x}_{2}} }{\lambda } \right).$
Độ lệch pha dao động đồng thời của m và n là $\delta \varphi =\frac{2\pi \left( {{x}_{2}}-{{ x} _{ 1} } \right)}{\lambda }.$
Nếu hai điểm m và n nằm trên cùng một đường truyền nhưng cách nhau một khoảng d thì ta có: $d={{x}_{2}}-{{x}_{1}}$
Độ lệch pha giữa 2 dao động tại m và n là $\delta \varphi =\frac{2\pi d}{\lambda }.$
Vậy coi sóng truyền cùng phương.
+) Khi hai điểm m và n cùng pha: $\delta \varphi =\frac{2\pi d}{\lambda }=k2\pi \leftrightarrow d=k λ .$
m, n gần nhau nhất khi $mn=\lambda .$
+) Khi hai điểm m và n lệch pha: $\delta \varphi =\frac{2\pi d}{\lambda }=\left( 2k+1 \right ) pi \leftrightarrow d=\left( k+0.5 \right)\lambda .$
m, n gần nhau nhất khi $mn=\frac{\lambda }{2}.$
+) Hai điểm m và n vuông góc với nhau khi: $\delta \varphi =\frac{2\pi d}{\lambda }=\left( k+\frac{1 } { 2} \right)\pi \leftrightarrow d=\left( 2k+1 \right)\frac{\lambda }{4}.$
Khi $mn=\frac{\lambda }{4}, m, n gần nhau nhất. $
2. Độ lệch pha của một điểm ở hai thời điểm khác nhau
Xét 2 điểm m cách nguồn một khoảng x.
Phương trình sóng tại m là ${{u}_{m}}=a\cos \left( \omega t-\frac{2\pi x}{\lambda } \ đúng). $
Điểm m gấp đôi ${{t}_{1}}$ và ${{t}_{2}}$$\left( {{t}_{2}} > ;{{t } _{1}} \right)$ là $\delta \varphi =\omega \left( {{t}_{2}}-{{t}_{1} } \right) = \omega \delta t.$
3. Độ lệch pha giữa m tại thời điểm ${{\text{t}}_{\text{2}}}$ và thời điểm n tại ${{t}_{1}}$
Đồng thời ${{t}_{1}}$ điểm m và n lệch pha nhau: $\frac{2\pi \left({{x}_{2}}- { {x}_ {1}} \right)}{\lambda }$
Tại thời điểm ${{t}_{2}}$ điểm m $\left( {{t}_{2}} \right)$ và điểm n$\left( { { t}_ {1}} \right)$ là:
$\delta \varphi =\omega .\left( {{t}_{2}}-{{t}_{1}} \right)+\frac{2\ pi \left( {{x}_{2}}-{{x}_{1}} \right)}{\lambda }.$
4. Xác định tính chất của các điểm m, n và hướng truyền sóng
A. Đặt câu hỏi
Bài toán: Xét hai điểm m và n có cùng phương truyền sóng, sóng truyền từ m đến n, $mn=d$. Trạng thái của m tại thời điểm ${{t}_{1}}$. Xác định thuộc tính của điểm n sau khoảng thời gian $\delta t$.
b. Cách giải quyết:
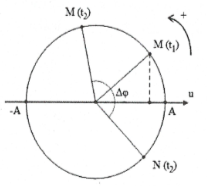
Sử dụng hình tròn tam giác
Chú ý sóng truyền từ m đến n nên điểm m chạy trước điểm n trên đường tròn tam giác (như hình vẽ).
Sau $\delta t$ta, chúng ta có thể xác định vị trí của điểm ${{m}_{2}}$. Dựa vào độ lệch pha giữa 2 điểm m và n để phán đoán trạng thái của điểm n.
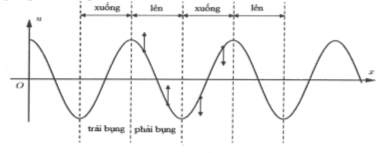
Chúng tôi nhận được kết quả: điểm bên trái của antinode dao động hướng xuống và điểm bên phải của antinode dao động hướng lên trên.
