Hình thoi là gì? Tính chất và công thức tính diện tích hình thoi

Hình thoi là kiến ​​thức chúng ta được tiếp xúc từ năm lớp 4. Trong quá trình học toán lớp 8, định nghĩa hình thoi đã được mở rộng và khắc sâu để trả lời các câu hỏi. Về tính chất của hình thoi, ý nghĩa của hình thoi, dấu hiệu nhận biết…, bài viết dưới đây hãy cùng ôn lại kiến ​​thức về hình thoi và luyện tập giải các dạng toán có liên quan

Định nghĩa hình thoi là gì?

hình thoi tiếng Anh là rhombus. Hình thoi là tứ giác có 4 cạnh bằng nhau.

• Hình thoi cũng là hình bình hành có 2 cặp cạnh đối bằng nhau hoặc là hình bình hành có 2 đường chéo vuông góc với nhau.
• Hình thoi có tất cả các tính chất của hình bình hành.

Lưu ý:

Hình thoi có bốn góc trong bằng nhau là hình vuông. Hình vuông là trường hợp đặc biệt của hình thoi vì nó có bốn cạnh bằng nhau và bốn góc vuông.

Hình thoi có những tính chất gì?

• Hình thoi có tất cả các tính chất của hình bình hành
• Hai đường chéo dọc
• Hai đường chéo là tia phân giác của góc hình thoi
• Hình thoi có các góc chéo bằng nhau, tổng các góc trong của hình thoi bằng 360 độ
• Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường
• Hai đường chéo là tia phân giác của các góc trong của hình thoi

Nhận biết hình thoi

Biểu trưng hình viên kim cương:

• Tứ giác có 4 cạnh bằng nhau
• Hình bình hành có hai cạnh bên bằng nhau
• Hình bình hành có hai đường chéo vuông góc với nhau
• Hình bình hành có đường chéo là tia phân giác của một góc

Công thức tính diện tích và chu vi hình thoi

Cho hình thoi abcd có độ dài cạnh a và độ dài hai đường chéo là d1 và d2



Công thức diện tích hình thoi

*Công thức tính diện tích hình thoi dựa trên 2 đường chéo

Diện tích hình thoi bằng một nửa tích độ dài hai đường chéo (1/2).

s = d1.d2

Ở đâu:

• s: diện tích hình thoi
• d1, d2: độ dài hai đường chéo của hình thoi

Công thức diện tích hình thoi dựa trên đáy và chiều cao



Diện tích hình thoi bằng một nửa (1/2) tích của chiều cao và cạnh bên

s = ½(a+a).h = a.h

Ở đâu:

• h: chiều cao của hình thoi
• a: cạnh dưới

*Công thức tính diện tích hình thoi dựa vào quan hệ trong tam giác (nếu biết góc của hình thoi)

s = a2. sina = a2. sinb = a2. sinc = a2. sind

Ở đâu:

• a: cạnh hình thoi

Công thức tính chu vi hình thoi

Chu vi hình thoi bằng độ dài một cạnh nhân với 4. 4 ở đây là 4 cạnh của hình thoi.

p = a.4

Ở đâu:

• p: chu vi hình thoi
• a: cạnh bất kỳ của hình thoi

Công thức tính đường chéo của hình thoi

Theo các công thức tính chu vi, diện tích hình thoi trên, ta được công thức tính đường chéo của hình thoi như sau:

* Tính đường chéo của hình thoi khi biết diện tích và độ dài của 1 đường chéo:

Nếu biết diện tích hình thoi và độ dài đường chéo (d1) thì ta dễ dàng tìm được các cạnh còn lại của hình thoi theo công thức sau:

d2= 2s / d1

Cách vẽ hình thoi nhanh gọn lẹ

Vẽ hình thoi abcd

Có hai phương pháp vẽ: thước kẻ và compa

Cách 1: Vẽ bằng thước

• Bước 1: Vẽ đoạn thẳng ac bất kì và xác định trung điểm o của đoạn thẳng ac.
• Bước 2: dùng eke vẽ đoạn thẳng bd vuông góc với ac tại o, tìm o là trung điểm của bd.
• Bước 3: Nối các đỉnh a với b, b với c, c với d, d với a => được hình thoi abcd.

Cách 2: Vẽ bằng thước

• Bước 1: Vẽ đoạn thẳng ac có độ dài bất kỳ.
• Bước 2: Sử dụng la bàn, mở rộng khẩu độ lên trên 12 ac. Vẽ cung có tâm là a và c, hai cung cắt nhau tại hai điểm gọi là b và d.
• Bước 3: Nối các điểm a, b, c, d với nhau => được hình thoi abcd.

Dạng bài tập hình thoi

Tính diện tích hình thoi có độ dài cạnh và độ dài đường chéo cho trước

Bài tập 1: Cho hình thoi abcd có chiều dài ab = 10 cm, đường chéo ac = 16 cm. Tính diện tích hình thoi abcd



Người chiến thắng:

Gọi o là giao điểm của hai đường chéo ac và bd , ta có oc = ½ ac = ½ . 16=8

Xét tam giác vuông boc ta có ob2= bc2- oc2=102-82=36 ⇒ ob=6(cm)

⇒db = 2.bo = 2,6 = 12

Diện tích hình thoi suy ra là sabcd=½ ac.bd = ½.12.16 = 96(cm2)

Tính diện tích hình thoi từ các góc và độ dài các cạnh kề

Ví dụ 2: Tính s-hình thoi abcd với góc a=30∘, biết ad=4cm,



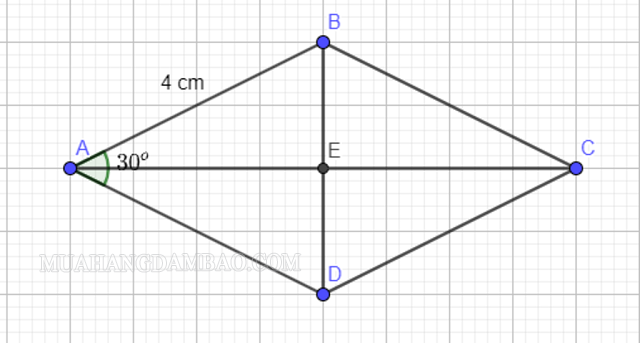
Người chiến thắng:

Vì abcd là hình thoi nên các tam giác đều cân.

Gọi e là trung điểm của 2 đường chéo. ⇒ae⊥bd và góc eab=15∘

Áp dụng định lý pitago vào abh ta có:

be2=ab2-ae2=42- 32⇒be = 7(cm)

⇒db = 2eb = 2√7(cm)

sabcd=2.sabd=2. ½ .bd.ae=2.½ 2√7.3 = 6√7 cm2

Trên đây là tổng hợp tất cả các kiến ​​thức liên quan đến hình thoi trong các môn Toán lớp 4, lớp 5, lớp 8. Hình thoi có ý nghĩa tạo tiền đề cho các phép tính diện tích, chu vi. Công thức liên quan cho hình vuông, hình chữ nhật, hình bình hành và các hình dạng khác. Khi đã có kiến ​​thức về hình thoi, việc áp dụng nó vào các dạng hình học khác sẽ dễ dàng và logic hơn rất nhiều. Hi vọng các bạn đã có những bài học thú vị và bổ ích