Giải bài 7, 8, 9 trang 69, 70 SGK Toán 9 tập 1 – Giaibaitap.me

Bài 7 Trang 69 SGK Toán 9 – Tập 1

Bạn Đang Xem: Giải bài 7, 8, 9 trang 69, 70 SGK Toán 9 tập 1 – Giaibaitap.me

bài 7. Người ta đưa ra 2 cách vẽ hai đoạn thẳng a, b lấy giá trị trung bình nhân với x (tức là \({x^2} = ab\) ) Như hình bên hai hình sau:

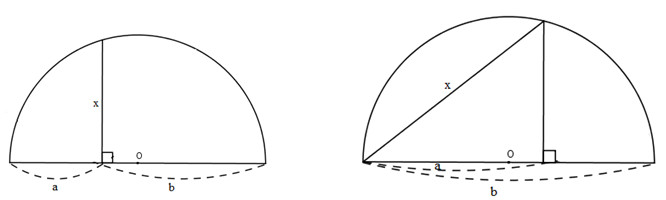
Theo quan hệ (1) và (2), hãy chứng minh rằng hình vẽ trên là đúng.

Gợi ý: Nếu trung tuyến của một cạnh của một tam giác bằng một nửa độ dài của cạnh đó thì tam giác đó là tam giác vuông.

Hướng dẫn giải quyết:

Cách 1: Đặt tên cho các hàng như hình bên dưới.

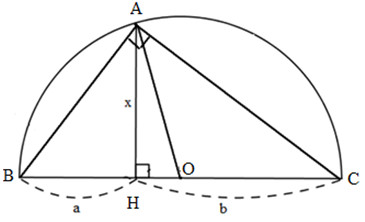
Xét tam giác abc ta có:

\(oa = ob = oc = {{bc} \over 2}\left( { = r} \right)\)

Xem Thêm : Giới Thiệu Nhà Thơ Đặng Trần Côn – Vanmau.com

Kết luận rằng abc là hình vuông tại a.

Áp dụng công thức \({h^2} = b’c’ \rightarrow {x^2} = ab\)

Xem Thêm: Tập làm văn lớp 5: Bài văn tả người hay nhất (312 mẫu) Bài văn tả người lớp 5

Cách 2: Vẽ và đặt tên cho hình sau

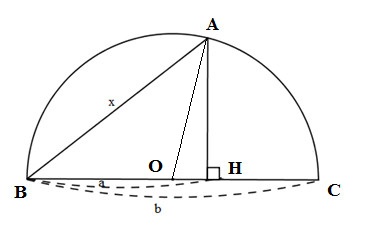
Xét tam giác abc ta có:

\(oa = ob = oc = {{bc} \over 2}\left( { = r} \right)\)

Xem Thêm : Giới Thiệu Nhà Thơ Đặng Trần Côn – Vanmau.com

Kết luận rằng abc là hình vuông tại a.

Áp dụng công thức \(a{b^2} = bc.bh \rightarrow {x^2} = ab\).

bài giảng 8 trang 70 sgk toán 9 – tập 1

Bài tập 8. Tìm x và y trong mỗi hình sau:

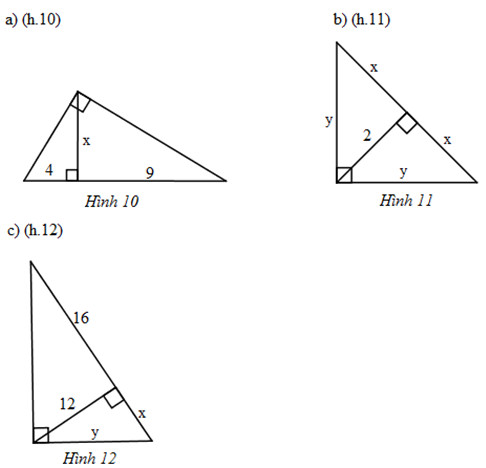
Hướng dẫn giải quyết:

a) Sử dụng phương trình đại số bậc hai, tích của hai hình chiếu của hai cạnh góc vuông trên cạnh huyền\(h^{2}=b’c’\)

\(\eqalign{ & \rightarrow {x^2} = 4,9 = 36 \cr & \rightarrow x = 6 \cr} \)

b) Xét tam giác abc có cạnh huyền 2x, ta thấy tam giác này là tam giác vuông cân. Mặt khác, chiều cao của tam giác này là 2, vì vậy:

Xem Thêm: Giải thích câu tục ngữ: Lá lành đùm lá rách – Văn mẫu lớp 8

\(\frac{1}{y^2}+\frac{1}{y^2}=\frac{1}{2^2}\rightarrow y=2\sqrt {2}\)

Cạnh huyền của tam giác lớn là 2x. Áp dụng định lý Pitago cho tam giác vuông lớn, ta có:

\(2x=\sqrt{y^2+y^2}=\sqrt{8+8}=4\rightarrow x=2\)

c) Xét tam giác vuông lớn, ta có:

\(12^2=16x\mũi tên phải x=9\)

Xét tam giác vuông có cạnh huyền y, ta có:

\(y^2=\sqrt{12^2+9^2}=15\)

Bài 9 Trang 70 SGK Toán 9 – Tập 1

Xem Thêm : Tổng hợp đề thi và đáp án chi tiết THPT QG môn tiếng Anh năm 2021

Sau 9. Hình vuông abcd. Gọi i là điểm nằm giữa a và b. Tia di cắt tia cb tại k. Vẽ đường thẳng vuông góc với di qua d. Đường thẳng này cắt đường thẳng bc tại l. bằng chứng

a) Tam giác dil là tam giác cân;

b) Tổng \(\frac{1}{di^{2}}+\frac{1}{dk^{2}}\) không đổi khi i thay đổi trên cạnh ab .

Hướng dẫn giải quyết:

Xem Thêm: Cách Làm Thịt Kho Quẹt Đậm Đà Vị Dân Dã

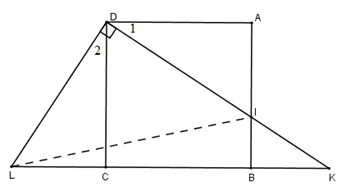
a) \(\delta adi\) và \(\delta cdl\) có:

\(\widehat{a}=\widehat{c}= 90^{\circ}\)

\(ad=cd\) (hai cạnh của hình vuông)

\(\widehat{d_{1}}=\widehat{d_{2}}\) và \(\widehat{cdi}\)

Do đó \(\delta adi=\delta cdl\) (g.c.g)

Suy ra \(di=dl\). Vì vậy \(\delta dil\) cân bằng

b) Áp dụng quan hệ \(\frac{1}{h^{2}}=\frac{1}{b^{2}}+\frac{1}{c^{2 } }\) Ta có \(\frac{1}{dc^{2}}=\frac{1}{dl^{2}}+\frac{1}{dk^{2 } } \)

Vậy \(\frac{1}{dc^{2}}=\frac{1}{di^{2}}+\frac{1}{dk^{2}} )

Vì dc là hằng số nên \(\frac{1}{di^{2}}+\frac{1}{dk^{2}}\) là hằng số.

Nhận xét: Câu a) chỉ là gợi ý để làm câu b). Điều cần chứng minh ở b) rất gần với hệ thức \(\frac{1}{h^{2}}=\frac{1}{b^{2}}+\frac{1 } {c^ {2}}\)

Nếu đề bài không cho phép vẽ \(dl\perp dk\) thì ta vẫn phải vẽ đường phụ \(dl\perp dk\) để áp dụng công thức trên.

giaibaitap.me