Bài 8: Cộng, Trừ Đa Thức Một Biến – Giải bài 44, 45, 46, 47 Trang 45; bài 48, 49, 50, 51, 52, 53 SGK Toán 7 Tập 2.
Để cộng và trừ hai đa thức một biến, chúng ta có thể thực hiện một trong hai cách sau:
Cách 1. Cộng, trừ các đa thức đã học ở Bài 6.
Cách 2. Sắp xếp các hạng tử của hai đa thức theo lũy thừa giảm (hoặc tăng) của các biến rồi thực hiện phép tính theo cột dọc tương tự như cộng, trừ các số (chú ý đặt các đơn thức đồng dạng) trong cùng một cột).
Gợi ý giải bài tập SGK Toán 7 tập 2: Cộng trừ đa thức một biến trang 43
bài 44.Cho hai đa thức: p(x) = -5×3 – 1/3 + 8×4 + x2 và q(x) = x2 – 5x – 2×3 + x4 – 2/3
Tính p(x) + q(x) và p(x) – q(x).
Đáp án: Ta có: p(x) = -5×3 – 1/3 + 8×4 + x2 và q(x) = x2 – 5x – 2×3 + x4 – 2/3. p>
Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:
Cuốn sách 45 Toán 7 Tập 2. Cho đa thức p(x) = x4 – 3×2 + 1/2 – x.
Tìm các đa thức q(x), r(x) sao cho:
a) p(x) + q(x) = x5 – 2×2 + 1.
b) p(x) – r(x) = x3.
Giải: Ta có: p(x) = x4 – 3×2 + 1/2 – x.
a) Vì p(x) + q(x) = x5 – 2×2 + 1 nên
q(x) = x5 – 2×2 + 1 – p(x)
q(x) = x5 – 2×2 + 1 – x4 + 3×2 – 1/2 + x
q(x) = x5 – x4 + x2 + x + 1/2
b) Vì p(x) – r(x) = x3 nên
r(x) = x4 – 3×2 + 1/2 – x – x3
Hoặc r(x) = x4 – x3 – 3×2 – x + 1/2
bài 46.Viết đa thức p(x) = 5×3 – 4×2 + 7x – 2 dưới dạng:
a) Tổng của hai đa thức một biến.
b) Hiệu của hai đa thức một biến.
bạn vinh nhận xét: “Ta có thể viết đa thức đã cho thành tổng của hai đa thức bậc 4”. đúng hay sai ? Tại sao?
Giải:Viết đa thức p(x) = 5×3 – 4×2 + 7x – 2 dưới dạng:
a) Tổng của hai đa thức một biến.
5×3 – 4×2 + 7x – 2 = (5×3 – 4×2) + (7x – 2)
b) Hiệu của hai đa thức một biến.
5×3 – 4×2 + 7x – 2 = (5×3 + 7x) – (4×2 + 2)
Chú ý: đáp án câu a; b không duy nhất, có thể tìm các đa thức khác.
Bạn nói đúng: chúng ta có thể viết đa thức đã cho dưới dạng tổng của hai đa thức bậc 4, ví dụ:
5×3 – 4×2 + 7x – 2 = (2×4 + 5×3 + 7x) + (- 2×4 – 4×2 – 2)
bài 47 trang 45 : Đối với đa thức:
p(x) = 2×4 -x – 2×3 + 1
q(x) = 5×2 – x3 + 4x
h(x) = -2×4 + x2 + 5.
Tính p(x) + q(x) + h(x) và p(x) – q(x) – h(x).
Chúng tôi có:
p(x) = 2×4 -x – 2×3 + 1
q(x) = 5×2 – x3 + 4x
h(x) = -2×4 + x2 + 5.
Sắp xếp các đa thức theo lũy thừa giảm dần rồi sắp xếp các hạng tử giống nhau về cùng một cột, ta được:
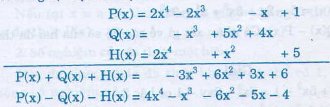
Sau 48:Hãy chọn đa thức mà em cho là đúng:
(2×3 – 2x + 1) – (3×2 + 4x – 1) = ?
(2×3 – 2x + 1) – (3×2 + 4x – 1) = 2×3 – 3×2 – 6x + 2.
Vậy chọn đa thức thứ hai.
Sau 4. Tìm bậc của mỗi đa thức sau:
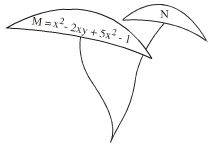
m = x2 – 2xy + 5×2 – 1
n = x2y2 – y2 + 5×2 – 3x2y + 5.
Đáp án: Đa thức m = x2 – 2xy + 5×2 – 1 = 6×2 – 2xy – 1 có bậc 2.
Đa thức n = x2y2 – y2 + 5×2 – 3x2y + 5 có bậc 4.
Bài 50, trang 46. Đối với đa thức:
n = 15y3 + 5y2 – y5 – 5y2 – 4y3 – 2y
m = y2 + y3 -3y + 1 – y2 + y5 – y3 + 7y5.
a) Rút gọn đa thức trên.
b) Tính n + m và n – m.
hd:a) Đa thức rút gọn:
n = 15y3 + 5y2 – y5 – 5y2 – 4y3 – 2y = -y5 + 11y3 – 2y
m = y2 + y3 -3y + 1 – y2 + y5 – y3 + 7y5 = 8y5 – 3y + 1.
b) n + m = -y5 + 11y3 – 2y + 8y5 – 3y + 1
= 7y5 + 11y3 – 5y + 1
n – m = -y5 + 11y3 – 2y – 8y5 + 3y – 1= -9y5 + 11y3 + y – 1.
bài 51 trang 46: Cho hai đa thức:
p(x) = 3×2 – 5 + x4 – 3×3 – x6 – 2×2 – x3;
q(x) = x3 + 2×5 – x4 + x2 – 2×3 + x – 1.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng dần của biến.
b) Tính p(x) + q(x) và p(x) – q(x).
hd:a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng dần của biến.
Gấp: p(x) = 3×2 – 5 + x4 – 3×3 – x6 – 2×2 – x3
= x2 – 5 + x4 – 4×3 – x6
Sắp xếp: p(x) = -5 + x2 – 4×3 + x4 – x6
Gấp: q(x) = x3 + 2×5 – x4 + x2 – 2×3 + x – 1= -x3 +2×5 – x4 + x2 + x – 1
Sắp xếp: q(x) = -1 + x + x2 – x3 – x4 + 2×5
b) Ta có:
Bài 52: Tính giá trị của đa thức p(x) = x2 – 2x – 8: x = -1; x = 0 và x = 4.
Giải: Ta có p(x) = x2 – 2x – 8
=> p(-1) = (-1)2 – 2 (-1) – 8 = 1 + 2 – 8 = -5.
p(0) = 02 – 2.0 – 8 = -8.
p(4) = 42 – 2,4 – 8 = 16 – 8 – 8 = 0.
bài 53 trang 46: Đối với đa thức:
p(x) = x5 – 2×4 + x2 – x + 1
q(x) = 6 -2x + 3×3 + x4 – 3×5.
Tính p(x) – q(x) và q(x) – p(x). Có nhận xét gì về hệ số của hai đa thức vừa tìm được?
Hướng dẫn giải pháp:
Chú ý: Ta thấy hệ số ứng với hai đa thức là đối nhau.
Chú ý: Ta gọi các hệ số ứng với hai đa thức là các đa thức đối nhau.
