Ví dụ 1:
Cho hình chóp s.abc có tam giác vuông abc tại b, \(ab=a \sqrt 2, ac=a \sqrt 3\), cạnh sa vuông góc với mặt đáy và \( sb =a \sqrt 3.\) Tính thể tích của hình chóp s.abc.
Giải pháp thay thế:
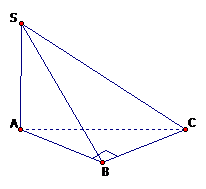
Tam giác abc vuông góc với b nên \(bc = \sqrt {a{c^2} – a{b^2}} = a.\)
Suy luận: \({{\rm{s}}_{\delta {\rm{abc}}}} = \frac{1}{2}ba.bc = \frac { 1}{2}.a\sqrt 2 .a = \frac{{{a^2}.\sqrt 2 }}{2}\)
Tam giác vuông sab tại a có \(sa = \sqrt {s{b^2} – a{b^2}} = a.\)
Vậy thể tích của hình chóp s.abc là: \({v_{s.abc}} = \frac{1}{3}.{s_{abc}}.sa = \frac{1 } {3}.\frac{{{a^2}.\sqrt 2 }}{2}.a = \frac{{{a^3}.\sqrt 2 }}{6}. )
Ví dụ 2:
Đối với hình chóp s.abcd, đáy abcd của nó là một hình vuông có cạnh \(a\sqrt2\), cạnh sa vuông góc với mặt phẳng của đáy và \(sc=a \sqrt5 \) .Tính thể tích của hình chóp s.abcd.
Giải pháp thay thế:
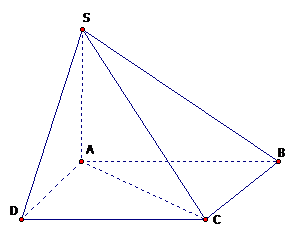
Vùng abcd: \({{\rm{s}}_{{\rm{abcd}}}} = {\left( {a\sqrt 2 } \right)^2 } = 2{a^2}.\)
Ta có: \(ac = ab.\sqrt 2 = a\sqrt 2 .\sqrt 2 = 2a.\)
Một tam giác vuông phải là: \(sa = \sqrt {s{c^2} – a{c^2}} = a\).
Vậy thể tích của hình chóp s.abcd là: \({v_{s.abcd}} = \frac{1}{3}.{s_{abcd}}.sa = \frac{1 } { 3}.2{a^2}.a = \frac{{2{a^3}}}{3}.\)
Ví dụ 3:
Cho hình chóp tam giác đều s.abc có đáy bằng \(a\sqrt3\) và cạnh bên bằng 2a, hãy tính thể tích của hình chóp s.abc.
Giải pháp thay thế:
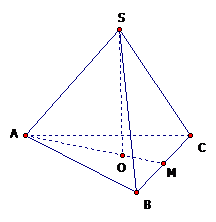
Gọi m là trung điểm của bc.
o là trọng tâm dẫn xuất của tam giác abc \(do đó \bot (abc).\)
Từ tam giác đều abc có độ dài cạnh \(a\sqrt3\) suy ra:
\(am=a\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{{3a}}{2}.\)
\({\rm{ao = }}\frac{{\rm{2}}}{{\rm{3}}}.am = \frac{2}{3} .\frac{{3a}}{2} = a\).
\({{\rm{s}}_{\delta {\rm{abc}}}} = \frac{1}{2}ab.ac.\sin {60^ 0} = \frac{1}{2}.a\sqrt 3 .a\sqrt 3 .\frac{{\sqrt 3 }}{2} = \frac{{3{a^2 }.\sqrt 3 }}{4}\).
Tam giác sao nằm chính xác tại a, vì vậy chúng ta có \(so = \sqrt {s{a^2} – a{o^2}} = a.\sqrt 3.\)
Vậy thể tích của khối chóp s.abc là:
\({v_{s.abc}} = \frac{1}{3}.{s_{abc}}.sa = \frac{1}{3}.\frac{{3 {a^2}\sqrt 3 }}{4}.a = \frac{{{a^3}.\sqrt 3 }}{4}.\)
Ví dụ 4:
Cho hình chóp vuông s.abcd có đáy abcd là cạnh a, cạnh bên sa vuông góc với mặt đáy và sc tạo với mặt đáy một góc 600. Tính thể tích của s.abcd.
Giải pháp thay thế:
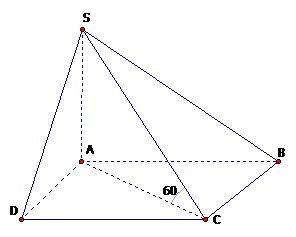
\(sa \bot (abcd)\) Vậy ac là hình chiếu của sc trên mặt phẳng (abcd).
Do đó: \(\widehat {(sc,(abcd))} = \widehat {(sc,ac)} = \widehat {sca} = {60^o}.\)
Diện tích đáy là: \({{\rm{s}}_{{\rm{abcd}}}} = {a^2}.\)
Tam giác vuông tại a có \(ac=a \sqrt2, \widehat {sca} = {60^0} \rightarrow sa = ac.\tan {60^o} = a sqrt 6.\)
Vậy thể tích của hình chóp là: \({v_{s.abcd}} = \frac{1}{3}.{s_{abcd}}.sa = \frac{1}{3 } . {a^2}.a\sqrt 6 = \frac{{{a^3}.\sqrt 6 }}{3}.\)
Ví dụ 5:
Cho tam giác vuông cân s.abc có đáy abc là a, cạnh \(bc=a\sqrt2,\) sa vuông góc với mặt phẳng đáy, mặt bên (sbc) và đáy (abc) tạo thành góc 450 độ. Tính thể tích của hình chóp s.abc.
Giải pháp thay thế:
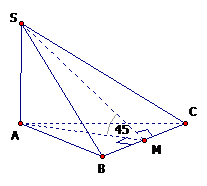
Gọi m là trung điểm của bc, ta có: \(am \bot bc\).
Mặt khác: \(sa \bot bc\) làm \(sa \bot \left( {abc} \right).\)
Nên: \(bc \bot (sam) \rightarrow sm \bot bc.\)
Khấu trừ: \(\widehat {((sbc),(abc))} = \widehat {(sm,am)} = \widehat {sma} = {45^o}\) .
Có \(bc=a\sqrt2\) trong tam giác abc và a vuông góc:
\(ab = bc = a\) và \(am = \frac{{a\sqrt 2 }}{2}\) \(\rightarrow {{\rm{ s}}_{\delta {\rm{abc}}}} = \frac{1}{2}ab.ac = \frac{1}{2}.a.a = \frac{{{ a^2}}}{2}\)
Tam giác vuông tại a có \(am = \frac{{a\sqrt 2 }}{2}\) và \(\widehat {sma} = {45^o} )
Suy luận: \(sa = ab.\tan {45^o} = \frac{{a\sqrt 2 }}{2}.\)
Vậy thể tích của khối chóp s.abc là:
\({v_{s.abc}} = \frac{1}{3}.{s_{abc}}.sa = \frac{1}{3}.\frac{{{ a^2}}}{2}.\frac{{a\sqrt 2 }}{2} = \frac{{{a^3}.\sqrt 2 }}{{12}}\ )
Ví dụ 6:
Cho lăng trụ đứng abc.a’b’c’, đáy abc của nó là tam giác vuông tại b, ab=a, \(ac=a\sqrt3\), cạnh a ‘ b = 2a. Tính thể tích abc.a’b’c’ của lăng trụ.
Giải pháp thay thế:
Tam giác abc vuông góc với b nên \(bc=\sqrt {a{c^2} – a{b^2}} = a\sqrt 2.\)
Suy luận: \({s_{abc}} = \frac{1}{2}ab.bc = \frac{{{a^2}\sqrt 2 }}{2}.\ )
Tam giác a’ab vuông góc với a nên:\(a’a = \sqrt {a'{b^2} – a{b^2}} = a\sqrt 3 . )
Vậy thể tích của lăng trụ là: \({v_{abc.a’b’c’}} = {s_{abc}}.a’a = \frac{{{a ) ^ 3}\sqrt 6 }}{2}.\)
Ví dụ 7:
Cho tam giác đều abc.a’b’c’ có đáy là \(2a\sqrt3\), hình chiếu đứng (abc) của a’ lên mặt phẳng và trọng tâm của tam giác abc Thật trùng hợp, cạnh a’a tạo với đáy (abc) một góc 300. Tính thể tích của lăng trụ đứng abc.a’b’c’.
Giải pháp thay thế:
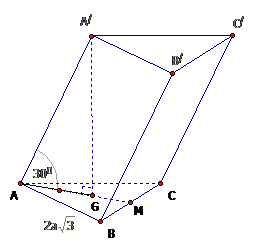
Gọi m là trung điểm của bc.
g là trọng tâm suy ra của tam giác abc: \(a’g \bot (abc)\).
Vậy ag là hình chiếu đứng của aa’ trên mặt phẳng (abc).
Suy ra: \(\left( {\widehat {{a^/}a,(abc)}} \right) = \widehat {{a^/}ag} = {30^ 0 }.\)
Tam giác đều abc có độ dài cạnh \(2a\sqrt3\) Vậy: \({s_{abc}} = {\left( {2a\sqrt 3 } \right)^ 2} .\frac{{\sqrt 3 }}{4} = 3{a^2}\sqrt 3.\)
Tam giác vuông a’ag tại g có \(\widehat a = {30^0},ag = \frac{2}{3}am = \frac{2}{3}. 2a\sqrt 3 .\frac{{\sqrt 3 }}{2} = 2a.\)
Suy luận: \(a’g = ag.\tan {30^0} = \frac{{2a\sqrt 3 }}{3}.\)
Vậy: \({v_{abc.{a’}{b’}{c’}}} = {s_{abc}}.{a’}a = 6{a^3 }.\)
Ví dụ 8:
Cho hình chóp s.abc có tam giác đều abc cạnh 2a, cạnh bên sa vuông góc với mặt phẳng đáy và \(sa=a\sqrt3.\)gọi m, n là trung điểm của mặt bên Các mặt phẳng cơ sở lần lượt là sb và sc. Tính thể tích của các hình chóp s.amn và a.bcnm.
Giải pháp:
.png)
Các đỉnh s.amn và s.abc có chung đỉnh s và góc tại đỉnh s.
Vậy theo công thức tỉ lệ thể tích, ta có:
\(\frac{{{v_{s.amn}}}}{{{v_{s.abc}}}} = \frac{{{\rm{sa}}}}{ {{\rm{sa}}}}.\frac{{sm}}{{sb}}.\frac{{sn}}{{sc}} = 1.\frac{1}{2 }.\frac{1}{2} = \frac{1}{4}\)
Suy luận: \({v_{s.amn}} = \frac{{{v_{s.abc}}}}{4} = \frac{{\frac{1}{3} .{a^2}\sqrt 3 .a\sqrt 3 }}{4} = \frac{{{a^3}}}{4}\)
Và: \({v_{a.bcnm}} = \frac{3}{4}.{v_{s.abc}} = {\frac{{3a}}{4}^3 }.\)
Ví dụ 9:
Cho hình chóp\(s.abcd\) có đáy là hình bình hành, m và n lần lượt là trung điểm của sa và sb. Tính tỷ lệ thể tích \(\frac{{{v_{s.cdmn}}}}{{{v_{s.cdab}}}}\).
Giải pháp thay thế:
.png)
Ta có:
\({v_{s.mncd}} = {v_{s.mcd}} + {v_{s.mnc}}\) và \({v_{s.abcd}} = {v_ {s.acd}} + {v_{s.abc}}\).
Sau đó: \(\frac{{{v_{s.mcd}}}}{{{v_{s.acd}}}} = \frac{{sm}}{{sa}} = \frac{1}{2} \leftrightarrow {v_{s.mcd}} = \frac{1}{4}{v_{s.abcd}}\)
Mặt khác: \(\frac{{{v_{s.mnc}}}}{{{v_{s.abc}}}} = \frac{{sm}}{{sa}}. \frac{{sn}}{{sb}} = \frac{1}{4} \rightarrow {v_{s.mnc}} = \frac{1}{8}{v_{s.abcd }}\)
Từ phía trên\({v_{s.mncd}} = \left( {\frac{1}{4} + \frac{1}{8}} \right){v_{s .abcd}} = \frac{3}{8}{v_{s.abcd}}\).
