Bài tập §4. Đường trung bình của tam giác, đường trung bình của hình thang Chương 1 – Tứ giác SGK Toán 8 1. Nội dung Luyện tập giải bài 26 27 28 trang 80 SGK Toán 8 Tập 1 SGK Toán hình học tổng hợp phần công thức, lý thuyết, phương pháp giải giúp học sinh học tốt môn Toán lớp 8.
Lý thuyết
1. Phần giữa của tam giác
Đường trung tuyến của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.
Định lý 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm của cạnh thứ ba.
Định lý 2: Đường trung tuyến của một tam giác thì song song với cạnh thứ ba và một nửa cạnh đó.
2. Đường tâm của hình thang
Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh của hình thang.
Định lý 3: Đường thẳng đi qua trung điểm một cạnh của hình thang và song song với hai đáy thì đi qua trung điểm của cạnh kia.
Định lý 4: Đường trung bình của hình thang thì song song với hai đáy thì bằng nửa tổng hai đáy.
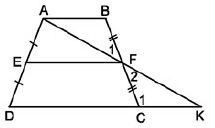
Dưới đây là phần hướng dẫn giải câu 26, 27, 28 trang 80 SGK Toán 8. Các em đọc kỹ bài 1 trước khi làm bài nhé!
Bài tập
giaibaisgk.com giới thiệu đến các em lời giải đầy đủ phần bài tập Hình học 8 và lời giải chi tiết SGK Toán 8 bài 4 trang 26 27 28 trang 80. Trong chương đầu tiên, tam giác của tứ giác và đường trung bình của hình thang dành cho các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 26 trang 80 SGK Toán 8 tập 1
Tính $x,y$ trên Hình 45, trong đó: $ab//cd//ef//gh$
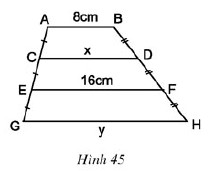
Giải pháp:
Ta có $ab//ef$ nên $abfe$ là hình thang
$\left.\begin{matrix} ca = ce\ db = df\end{matrix}\right\}$
⇒ $ad$ là đường trung bình của hình thang $abfe$
Do đó: $cd = \frac{ab + ef}{2} = \frac{8 + 16}{2} = 12$
Vậy $x = 12cm$
Tương tự, ta có $cd//gh$ nên $cdhg$ là một hình thang.
$\left.\begin{matrix} ec = eg\\ fd = fh\end{matrix}\right\}$
⇒ $ef$ là đường trung bình của hình thang $cdhg$
Do đó: $ef = \frac{cd + gh}{2}$ ⇒ $gh = 2.ef – cd = 2,16 – 12 = 20$
Vậy $y = 20cm$
2. Giải bài 27 trang 80 sgk toán 8 tập 1
Cho tứ giác $abcd$. Gọi $e, f, k$ lần lượt là trung điểm của $ad, bc, ac$
.
a) So sánh độ dài của $ek$ và $cd, kf$ và $ab$
b) chứng minh rằng $ef \leq \frac{ab + cd}{2}$
Giải pháp:
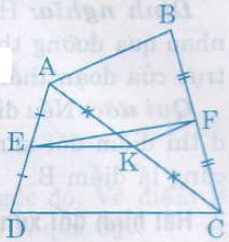
a)Chúng tôi có
$\left.\begin{matrix} ea = ed\\ ka = kc\end{matrix}\right\}$
⇒ $ek$ là đường trung bình của tam giác $acd$
Vậy $ek = \frac{cd}{2}$
Tương tự ta có:
$\left.\begin{matrix} fb = fc\\ ka = kc\end{matrix}\right\}$
⇒ $kf$ là đường trung tuyến của tam giác $abc$
Vậy $kf = \frac{ab}{2}$
b) Trong tam giác $efk$ ta có:
$ef \leq ek + kf$
$⇔ ef \leq \frac{cd}{2} + \frac{ab}{2}$
⇒ $ef \leq \frac{ab + cd}{2}$ (dpcm)
3. Giải bài 28 trang 80 SGK toán 8 tập 1
Đối với hình thang $abcd (ab//cd), e$ là trung điểm của $ad và f$ là trung điểm của $bc$. Đường thẳng $ef$ cắt $bd$ tại $i$ và $ac$ tại $k$
a) Chứng minh rằng $ak = kc, bi = id$
b) $ab = 6cm, cd = 10cm$. Tính độ dài $ei, kf, ik$
Giải pháp:
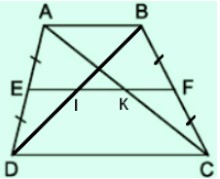
a)Chúng tôi có:
$\left.\begin{matrix} ea = ed\\ fb = fc\end{matrix}\right\}$
⇒ $ef$ là đường trung bình của hình thang $abcd.$
Do đó $ef // ab // cd$
Tam giác $abc$ có:
$\left.\begin{matrix} kf // ab\\ fb = fc\end{matrix}\right\}$ ⇒ $ak = kc$
Tam giác abd có:
$\left.\begin{matrix} ea = ed\\ ei // ab\end{matrix}\right\}$ ⇒ $bi = id$
b)Ta có:
ef là đường trung bình của hình thang abcd nên:
$ef = \frac{ab + cd}{2} = \frac{6 + 10}{2} = 8$
ei là trung tuyến của tam giác abd nên:
$ei = \frac{ab}{2} = \frac{6}{2} = 3$
kf là đường trung tuyến của tam giác abc nên:
$kf = \frac{ab}{2} = \frac{6}{2} = 3$
Ta cũng có $ef = ei + ik + kf$
$ ⇒ ik = ef – (ei + kf) = 8 – (3 + 3) = 2$
Vậy $ei = kf = 3cm, ik = 2cm$
Trước:
- Giải bài 20 21 22 23 24 25 trang 79 80 SGK Toán 8 tập 1
- Giải bài 29 30 31 tr.83 SGK Toán 8 1
- Câu hỏi khác 8
- Học tốt vật lý lớp 8
- Học tốt môn sinh học lớp 8
- Học tốt ngữ văn lớp 8
- Điểm tốt môn lịch sử lớp 8
- Học tốt môn địa lý lớp 8
- Học tốt tiếng Anh lớp 8
- Học tốt môn tiếng Anh lớp 8 thí điểm
- Học Khoa học Máy tính Lớp 8
- Học chăm chỉ môn gdcd lớp 8
Tiếp theo:
Xem thêm:
<3
“Môn thể thao nào đã khó giabaisgk.com”
