Bài tập §4. Hai tam giác đồng dạng, Chương 3 – Tam giác đồng dạng, SGK Toán 8 Tập 2. SGK Toán 8 Tập 2, bài 26, bài 27 trang 72 Bài giải bao gồm công thức, lý thuyết và các phương pháp giải toàn diện các bài tập trong phần hình học SGK Toán 8, giúp học sinh học tốt môn Toán lớp 8.
Lý thuyết
1. định nghĩa
Tam giác a’b’c’ được coi là đồng dạng với tam giác ab nếu:
\(\begin{array}{l} \widehat {a’} = \widehat a;\,\,\,\,\widehat {b’} = \ widehat b;\,\,\,\,\widehat {c’} = \widehat c;\\ \frac{{a’b’}}{{ab}} = frac{{a’c’}}{{ac}} = \frac{{b’c’}}{{bc}} \end{array}\)
Ký hiệu: \(\delta a’b’c’ \sim \delta abc\) .
Tỷ số của cạnh tương ứng là \(\frac{{a’b’}}{{ab}} = \frac{{a’c’}}{{ac}} = \frac {{ b’c’}}{{bc}} = k\) được gọi là tỷ lệ đồng dạng.
Chú ý: Khi viết các kí hiệu đồng dư ta viết theo thứ tự các cặp đỉnh tương ứng.
Một số thuộc tính:
Mỗi tam giác đồng dạng với chính nó.
Nếu \(\delta a’b’c’\sim\delta abc\) thì \(\delta abc\sim\delta a’b’c’\).
Nếu \(\delta a”b”c”\sim\delta a’b’c’\) và \(\delta a”b”c”\sim\delta abc\) rồi \(\delta abc\sim\delta a’b’c’\).
2. Định lý
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh kia thì tạo thành một tam giác mới giống tam giác đã cho.
Sau đây là hướng dẫn Giải bài tập trang 72, 26, 27, 28 SGK Toán 8. Các em hãy đọc kỹ bài đầu tiên trước khi làm các câu hỏi nhé!
Bài tập
giaibaisgk.com giới thiệu đến các em lời giải đầy đủ các bài tập hình học trong tiết 8 và lời giải chi tiết SGK Toán 8 bài 4 trang 72 bài 26 27 28. Hai tam giác đồng dạng trong Chương 3 – Tam giác đồng dạng để các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 26 trang 72 SGK Toán 8 tập 2
Cho tam giác \(abc\) vẽ tam giác \(a’b’c’\) đồng dạng với tam giác \(abc\) theo tỉ số đồng dạng \(k = \)dfrac {2}{3}\)
Giải pháp thay thế:
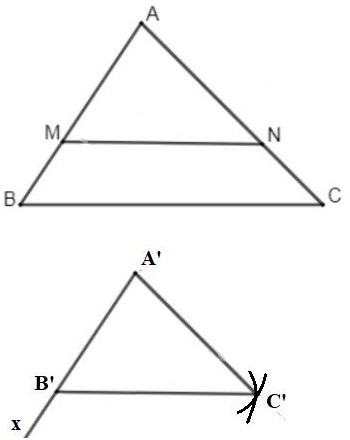
Lấy điểm \(m\) trên cạnh \(ab\) sao cho \(am= \dfrac{2}{3}ab.\)
Vẽ một đường thẳng song song với \(bc\) từ \(m\) và cắt \(ac\) tại \(n\).
Ta có \(Δamn\) ∽ \(Δabc\) với phép đồng dạng \(k=\dfrac{2}{3}\)
♦ Dựng \(Δa’b’c’ = Δamn\) (theo các trường hợp cạnh)
– Dựng tia \(a’x\), lấy \(b’\) trên tia \(a’x\) sao cho \(a’b’ = am\)
– Dựng các cung có tâm \(a’\) và bán kính \(an\) và các cung có tâm \(b’\) và bán kính \(mn\) Cung, hai cung cắt nhau tại (c’\)
– Ghép \(a’c’, b’c’\) ta được tam giác \(a’b’c’\) cần dựng.
Tỷ số đồng dạng của \(Δamn\) ∽ \(Δabc\) là \(k=\dfrac{2}{3}\) nên \(Δa’ b ‘c’ \) ∽ \(Δabc\) tương tự\(k=\dfrac{2}{3}\).
2. Giải bài 27 trang 72 SGK Toán 8 Tập 2
m thuộc cạnh ab của tam giác abc, $am= \frac{1}{2}.mb$. Vẽ các tia song song với ac, bc cắt bc và ac lần lượt tại l và n.
a) Kể tên tất cả các cặp tam giác đồng dạng.
b) Với mỗi cặp tam giác đồng dạng, hãy viết các cặp tam giác đồng dạng và tỉ số đồng dạng tương ứng.
Bài giải: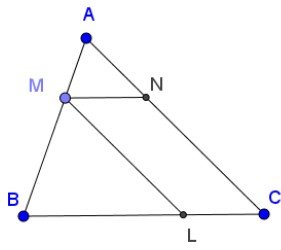 
a) Trong tam giác abc có:
mn // bc (gt) amn abc (định lý) (1)
ml // ac (gt) mbl abc (định lý) (2)
Từ (1) (2) amn mlb (thuộc tính)
b) Ta có:
Δamn ∽ Δabc ⇒ \(\widehat{amn} = \widehat{abc}; \widehat{anm} = \widehat{acb}\)
Và tỷ lệ tương đồng: \(k_1=\frac{am}{ab} = \frac{1}{3}\)
Δmbl ∽ Δabc ⇒ \(\widehat{mbl} = \widehat{bac},\widehat{mlb}= \widehat{acb}\)
Và tỷ lệ tương đồng: \(k_2=\frac{mb}{ab} = \frac{2}{3}\)
Δamn mlb có:
\(\widehat{man} = \widehat{bml}, \widehat{amn} = \widehat{mbl}, \widehat{anm} = \widehat{mlb}\)
Và tỷ lệ tương đồng: \(k_3=\frac{am}{mb}= \frac{1}{2}\)
3. Giải bài 28 trang 72 SGK Toán 8 tập 2
\(Δa’b’c’\) ∽ \(Δabc\) trong hệ số đồng dạng \(k= \dfrac{3}{5}\).
a) Tính tỉ số chu vi của hai tam giác đã cho.
b) Cho biết chu vi của hai tam giác trên là \(40\)dm, hãy tính chu vi của mỗi tam giác đó.
Giải pháp thay thế:
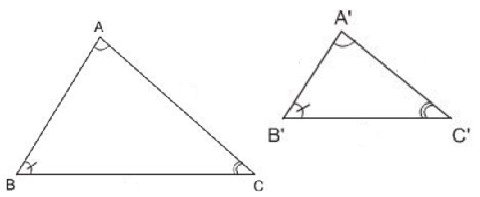
a) \(Δa’b’c’\) ∽ \(Δabc\) tương tự\(k= \dfrac{3} {5} \ ) (gt)
\( \rightarrow \dfrac{a’b’}{ab} = \dfrac{b’c’}{bc} = \dfrac{c’a’}{ca} = \ dfrac{3}{5}\) (tính chất của hai tam giác đồng dạng)
Áp dụng tính chất của chuỗi hình học:
\(\dfrac{{a’b’}}{{ab}} = \dfrac{{b’c’}}{{bc}} = \dfrac{{c’a’} {{ca}}\)\(\,= \dfrac{a’b’+b’c’+c’a’}{ab+bc+ca}\)\(\ , = \dfrac{c_{a’b’c’}}{c_{abc}}= \dfrac{3}{5}\)
Vậy tỉ số chu vi của \(Δa’b’c’\) và \(Δabc\) là \(\dfrac{3}{5}\).
b) Vì \(\dfrac{c_{a’b’c’}}{c_{abc}}= \dfrac{3}{5}\) (c_{abc}- c_{a’b’c’} = 40\,dm\)
Áp dụng tính chất của chuỗi hình học:
\( \dfrac{c_{abc}}{5}= \dfrac{c_{a’b’c’}}{3} \)\(\,=\dfrac{ {{c_{abc}} – {c_{a’b’c’}}}}{{5 – 3}}\)\(\,= \dfrac{40}{2}= 20 )
\( \rightarrow c_{abc}= 5.20=100\, dm\)
\(c_{a’b’c’}= 20.3=60\, dm\)
Trước:
- Giải bài 23 24 25 trang 71 72 SGK Toán 8 Tập 2
- Giải bài 29 30 31 trang 74 75 SGK Toán 8 tập 2
- Câu hỏi khác 8
- Học tốt vật lý lớp 8
- Học tốt môn sinh học lớp 8
- Học tốt ngữ văn lớp 8
- Điểm tốt môn lịch sử lớp 8
- Học tốt môn địa lý lớp 8
- Học tốt tiếng Anh lớp 8
- Học tốt môn tiếng Anh lớp 8 thí điểm
- Học Tin học lớp 8
- Học chăm chỉ môn gdcd lớp 8
Tiếp theo:
Xem thêm:
<3
“Bài tập nào khó, đã có giabaisgk.com”
