Bài tập §3. Lượng giác, Chương 1 – Hệ hàm số lượng giác trong tam giác vuông, SGK Toán 9, tập 1, tr. Nội dung Giải bài 20 21 22 23 24 25 trang 84 SGK Toán 9 Tập 1 bao gồm các bài giải tổng hợp về công thức, lý thuyết và phương pháp giải bài tập trong phần Hình học trong SGK Toán 9, giúp học sinh học tốt môn Toán lớp 9.
Lý thuyết
1. Cấu trúc bảng lượng giác
Bảng lượng giác bao gồm bảng viii, bảng ix, bảng x Brazil của sách “Bảng số có 4 chữ số thập phân”
Mọi người tạo bảng dựa trên các thuộc tính:
Nếu hai góc \(\alpha\) và \(\beta\) bù nhau (\(\alpha +\beta=90^{\circ}\) ) Sau đó \(sin\alpha =cos\beta ,cos\alpha =sin\beta ,tan\alpha =cot\beta ,cot\alpha =tan\beta\)
– Bảng viii dùng để tính sin và cosin của các góc nhọn, cũng như tính các góc khi biết sin và cosin của một góc. Có 16 cột và hàng
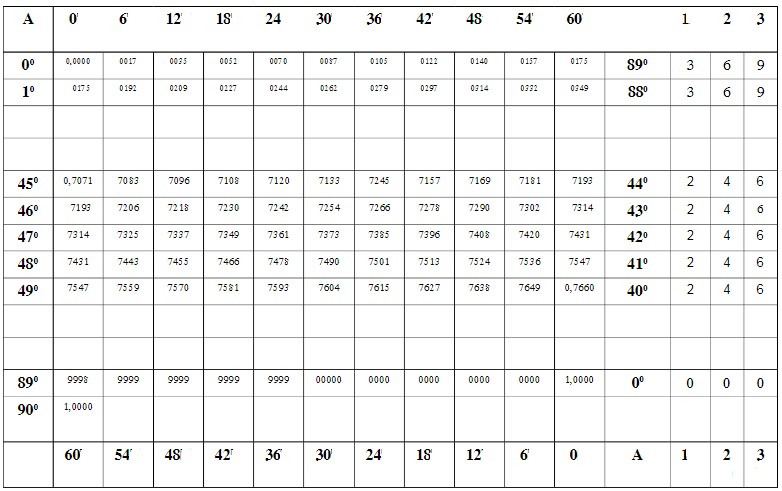
Cột 1 và 13 ghi độ nguyên. Cột 1 ghi độ tăng từ \(0^{\circ}\) đến \(90^{\circ}\) từ trên xuống dưới, cột 13 ghi giảm ngược lại.
3 cột cuối của bản ghi dùng để hiệu chỉnh giá trị của các góc khác nhau 1′, 2′, 3′
– Bảng ix dùng để tìm góc tan từ \(0^{\circ}\) đến \(76^{\circ}\) và giá trị của góc cot từ \ ( 14^{\circ}\) đến \(90^{\circ}\) và ngược lại, tìm góc khi biết tan và cot. Cấu trúc tương tự như Bảng viii.
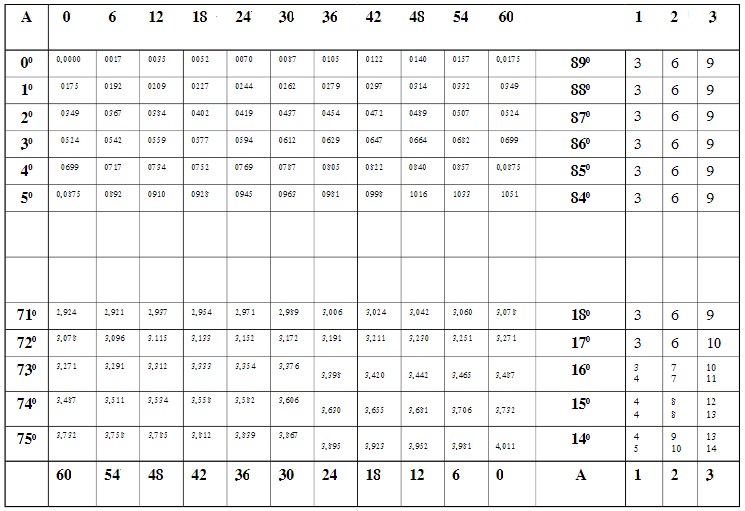
– Bảng x dùng để tìm giá trị tan của góc \(76^{\circ}\) đến \(89^{\circ}59{}’\) và góc cot là tiếp tuyến và phần dư Khi biết tiếp tuyến, hãy tìm góc nhọn từ \(1{}’\) đến \(14^{\circ}\) và ngược lại.
2. Cách sử dụng biểu mẫu
a) Tính tỉ số lượng giác của một góc nhọn cho trước
Bước 1: Tìm hoành độ của sin và tiếp tuyến ở cột 1 (côsin và cosin ở cột 13).
Bước 2: Tìm sin và tiếp tuyến theo phút ở dòng 1 (cos và cotang ở dòng cuối cùng).
Bước 3: Lấy giá trị giao hàng, ghi độ, ghi biên bản vào một cột.
b) Tìm tung độ góc nhọn của tỉ số lượng giác
Sử dụng bảng thích hợp để tìm tỉ số lượng giác, sau đó căn cột độ và phút theo tỉ số đó. Ta sẽ được số đo các góc cần tìm.
Sau đây là hướng dẫn Giải bài tập 1 SGK Toán 9 trang 20 21 22 23 24 25 và trang 84. Các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các em lời giải đầy đủ phần bài tập Hình học 9 và lời giải chi tiết SGK Toán 1 bài 3 trang 20 21 22 23 24 25 trang 84. Chương 1 Bảng Hàm Số Lượng Giác – Hệ thức Lượng giác Tam giác vuông để các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 20 trang 84 SGK Toán 9 Tập 1
Dùng bảng tam giác (có chỉnh sửa) hoặc máy tính bỏ túi, tìm các tỷ số tam giác sau (làm tròn đến bốn chữ số thập phân):
a) sin $70^0$13′ ; b) cos $25^0$32′ ;
c) tg $43^0$10′ ; d) chi phí $32^0$15′
Giải pháp:
a) $sin 70^013’ \xấp xỉ 0,9410$
b) $cos 25^032’ \xấp xỉ 0,9023$
c) $tg 43^010’ \xấp xỉ 0,9380$
d) $cotg 32^015’ \xấp xỉ 1,5849$
2. Giải bài 21 trang 84 sgk toán 9 tập 1
Dùng lượng giác hoặc máy tính bỏ túi để tìm góc nhọn x (làm tròn đến độ gần nhất), biết:
a) $sin x = 0,3495 $; b) $cos x = 0,5427$ ;
c) $tg x = 1,5142$; d) $cotg x = 3,163$.
Giải pháp:
a) $sin x = 0,3495 ⇒ x \khoảng 20^0$
b) $cos x = 0,5427 ⇒ x \xấp xỉ 57^0$
c) $tg x = 1,5142 ⇒ x \khoảng 57^0$
d) $cotg x = 3,163 ⇒ x \khoảng 18^0$
3. Giải bài 22 trang 84 sgk toán 9 tập 1
So sánh
a) sin $20^0$ và sin $70^0$; b) cos $25^0$ và cos $63^0$15’
c) tg $73^0$20′ và tg $45^0$; d) chi phí $2^0$ và chi phí $37^0$40′
Giải pháp:
Ta có: khi góc $\alpha$ tăng từ $0^0$ lên $90^0$ thì sin $\alpha$ và tg $\alpha$ tăng, còn cos $\alpha$ và cotg $ alpha$ giảm.
a) $20^0 < 70^0$ nên $sin 20^0 <sin 70^0$
b) $25^0 vì 63^015’$
c) $73^0 > 45^0$ nên $tg 73^020’ > 45^0$
d) $2^0 có giá 37^040’$
4. SGK Toán 9 Trang 84 Đáp án 23 Tập 1
Đếm
a) $\frac{sin 25^0}{cos 65^0}$ ;
b) $tg 58^0 – cotg 32^0$.
Giải pháp:
a) Vì các góc $25^0$ và $65^0$ là các góc bù nhau nên $cos 65^0 = sin 25^0$. Vì vậy, chúng tôi có:
$\frac{sin 25^0}{cos 65^0} = \frac{sin 25^0}{sin 25^0} = 1$
b) Vì góc $58^0$ và góc $32^0$ là hai góc kề bù nên $cotg 32^0 = tg 58^0$. Vì vậy, chúng tôi có:
$tg 58^0 – cotg 32^0 = tg 58^0 – tg 58^0 = 0$
5. Giải bài 24 trang 84 SGK Toán 9 Tập 1
Sắp xếp các tỉ số lượng giác sau theo thứ tự tăng dần:
a) sin $78^0$, cos $14^0$, sin $47^0$, cos $87^0$.
b) Chi phí $73^0$, chi phí $25^0$, chi phí $62^0$, chi phí $38^0$.
Giải pháp:
a)Chúng tôi có:
\(\cos 14^{\circ}=\sin(90^o – 14^o)=\sin 76^{\circ}\);
\(\cos 87^{\circ}=\sin (90^o – 87^o)=\sin 3^{\circ}.\).
Bởi vì \( 3^o < 47^o < 76^o < 78^o\)
\(\rightarrow \sin 3^{\circ}< \sin 47^{\circ}< \sin 76^{\circ}< \sin 78^ {\circ}\)
\(\rightarrow \cos 87^{\circ}< \sin 47^{\circ}< \cos 14^{\circ} < \sin 78^ o\).
b)Ta có:
\(\cot 25^{\circ}=\tan (90^o – 25^o)=\tan 65^{\circ}; \)
\(\cot 38^{\circ}=\tan (90^o – 38^o)=\tan 52^{\circ}\).
Bởi vì \(52^o < 62^o < 65^o < 73^o\)
\(\rightarrow \tan 52^{\circ}< \tan 62^{\circ}< \tan 65^{\circ}< \tan 73^ {\circ}\);
\(\rightarrow \cot 38^{\circ}< \tan 62^{\circ}< \cot 25^{\circ}< \tan 73^ {\circ}\).
6. Giải bài 25 trang 84 SGK Toán 9 Tập 1
So sánh
a) tg $25^0$ và sin $25^0$ ; b) cotg $32^0$ và cos $32^0$
c) tg $45^0$ và cos $45^0$; d) chi phí $60^0$ và tội lỗi $30^0$
Giải pháp:
♦ Cách 1:
Áp dụng thuộc tính sin $\alpha$ < tg $\alpha$, cos $\alpha$ < cotg $\alpha$. Chúng tôi có:
a) tg $25^0$ >sin $25^0$
b) giá $32^0$ >vì $32^0$
c) cos $45^0$ = sin $45^0$ nhưng tg $45^0$ >; sin $45^0$ nên tg $45^0$ >vì $45^0$
d) cos $60^0$ = sin $30^0$ mà cos $60^0$ >; cos $60^0$ nên cos $60^0$ >sin $30^0$p>
♦ Cách 2:
a) Ta có \(\tan 25^o = \dfrac{\sin 25^o}{\cos 25^o}\). Bởi vì \(0< \cos 25^o < 1\)
\(\rightarrow \dfrac{1}{\cos 25^o} > 1\)
\(\leftrightarrow \sin 25^o . \dfrac{1}{\cos 25^o} > \sin 25^o\).
\(\leftrightarrow \dfrac{\sin 25^o}{\cos 25^o} > \sin 25^o\).
\(\leftrightarrow \tan 25^o > \sin 25^o\).
b) Ta có: \(\cot 32^o = \dfrac{\cos 32^o}{\sin 32^o}\). Vì \(0< \sin 32^o < 1\)
\(\rightarrow \dfrac{1}{\sin 32^o} > 1\)
\(\leftrightarrow \cos 32^o. \dfrac{1}{\sin 32^o} > 1.\cos 32^o\)
\(\leftrightarrow \dfrac{\cos 32^o}{\sin 32^o} > \cos 32^o\)
\(\leftrightarrow \cot 32^o > \cos 32^o\).
c) Ta có \(\tan 45^o = \dfrac{\sin 45^o}{\cos 45^o}\). Vì \(0< \cos 45^o < 1\)
\(\rightarrow \dfrac{1}{\cos 45^o} > 1\)
\(\leftrightarrow \sin 45^o . \dfrac{1}{\cos 45^o} > \sin 45^o\).
\(\leftrightarrow \dfrac{\sin 45^o}{\cos 45^o} > \sin 45^o\).
\(\leftrightarrow \tan 45^o > \sin 45^o\)
Sau đó \(\sin 45^o= \cos(90^o – 45^o)=\cos 45^o\)
Vậy \( \tan 45^o > \cos 45^o\).
d) Ta có: \(\cot 60^o = \dfrac{\cos 60^o}{\sin 60^o}\). Vì \(0< \sin 60^o < 1\)
\(\rightarrow \dfrac{1}{\sin 60^o} > 1\)
\(\leftrightarrow \cos 60^o. \dfrac{1}{\sin 60^o} > 1.\cos 60^o\)
\(\leftrightarrow \dfrac{\cos 60^o}{\sin 60^o} > \cos 60^o\)
\(\leftrightarrow \cot 60^o > \cos 60^o \).
\(\cos 60^o = sin (90^o -60^o) = \sin 30^o\)
Do đó \( \cot 60^o > \sin 30^o\).
Trước:
- Giải bài 18 19 trang 83 84 SGK Toán 9 Tập 1
- 26 27 trang 88 SGK Toán 9 Tập 1
- Câu hỏi khác 9
- Học tốt vật lý lớp 9
- Học tốt môn sinh học lớp 9
- Học tốt ngữ văn lớp 9
- Điểm tốt môn lịch sử lớp 9
- Học tốt môn địa lý lớp 9
- Học tốt tiếng Anh lớp 9
- Tiếng Anh lớp 9 thí điểm
- Học Khoa học Máy tính Lớp 9
- Học tốt GDCD lớp 9
Tiếp theo:
Xem thêm:
Chúc các em tham khảo và giải bài tập 20 21 22 23 24 25 trang 84 SGK Toán 9 tập 1 thành công!
“Bài tập nào khó, đã có giabaisgk.com”
