Bài tập §2. Hàm Số Bậc Nhất Chương 2 – Hàm Số Bậc Nhất SGK Toán 9 I. 11 12 13 14 trang 48 sgk toán 9 tập 1 có nội dung tổng hợp các công thức, lý thuyết và phương pháp giải các bài toán trong phần đại số trong sách giáo khoa toán, giúp học sinh học tốt môn Toán lớp 9.
Lý thuyết
1. Khái niệm hàm số bậc nhất
Hàm bậc nhất là một hàm được cho bởi công thức \(y=ax+b\), trong đó \(a\) và \(b\) là các số đã cho và \ (a\neq 0\).
2. thuộc tính
Hàm \(y=ax+b(a\neq 0)\) xác định tất cả các giá trị của x trong \(\mathbb{r}\) và có các tính chất sau:
a) đồng biến trên \(\mathbb{r}\) khi a >; 0.
b) Đảo ngược \(\mathbb{r}\) khi < 0.
Dưới đây là hướng dẫn Giải bài tập 1, tập 9, tập 1, trang 11, 12, 13, 14 trang 48 SGK Toán, các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các em phương pháp giải bài tập Đại số 9 đầy đủ và đáp án chi tiết §2 trang 11 12 13 14 SGK Toán 9 tập 1. Hàm số bậc nhất trong chương 2 – Hàm số bậc nhất dành cho các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 11 trang 48 SGK Toán 9 tập 1
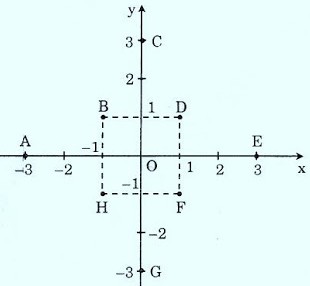
Hãy biểu diễn các điểm sau trên mặt phẳng tọa độ: a(-3; 0), b(-1; 1), c(0; 3), d(1; 1), e(3; 0 ), f(1; -1), g(0; -3), h(-1; -1).
Giải pháp:
+) tọa độ điểm \(a(-3; 0) \rightarrow\) tọa độ \(-3\) tọa độ \(0\)
\(\rightarrow \) Điểm \(a\) nằm trên trục hoành tại điểm \(-3\).
+) tọa độ điểm \(b(-1; 1) \rightarrow\) tọa độ \(-1\) tọa độ \(1\)
+) điểm \(c(0; 3) \rightarrow\) tọa độ \(0\), tọa độ là \(3\)
\(\rightarrow \) Điểm \(c\) nằm trên trục tung tại điểm \(3\).
+) điểm \(d(1; 1) \rightarrow\) tại \(1\) tại \(1\)
+) Điểm \(e(3; 0) \rightarrow\) tại \(3\) tại \(0\)
\(\rightarrow \) Điểm \(e\) nằm trên trục hoành tại điểm \(3\).
+) điểm \(f(1; -1) \rightarrow\) tại \(1\) tại \(-1\)
+) tọa độ điểm \(g(0; -3) \rightarrow\) là \(0\) tọa độ là \(-3\)
\(\rightarrow \) Điểm \(c\) nằm trên trục tung tại điểm \(-3\).
+) tọa độ điểm \(h(-1; -1) \rightarrow\) tọa độ \(-1\) tọa độ \(-1\)
Một điểm được biểu diễn trên mặt phẳng tọa độ như sau:
2. Giải bài 12 trang 48 SGK Toán 9 Tập 1
Đối với hàm bậc nhất $y = ax + 3$. Tìm hệ số $a$ biết rằng $y = 2,5.$ khi $x = 1$
Giải pháp:
Thay thế \(x=1,\ y=2,5\) vào công thức hàm trên để được:
\( 2.5=1.a+3 \)
\(\leftrightarrow 2.5= a+3 \)
\(\leftrightarrow a=3-2,5\)
\(\leftrightarrow a=0.5\).
Vậy \(a=0,5\) và hàm số là \(y=-0,5x+3\).
3. giải bài 13 trang 48 sgk toán 9 tập 1
Bậc đầu tiên của mỗi hàm số sau với giá trị của m là bao nhiêu?
a) $y = \sqrt{5 – m}(x – 1);$
b) $y = \frac{m + 1}{m – 1}x + 3,5$
Giải pháp:
Một hàm là hàm bậc nhất phải có dạng $y = ax + b$, trong đó $a ≠ 0.$
Do đó:
a) Ta có \(y=\sqrt{5 – m}(x – 1) \leftrightarrow y=\sqrt{5 – m}.x – \ căn bậc hai {5 – m} \)
\(\rightarrow\) hệ số là \(a=\sqrt{5-m}\).
Điều kiện để \(y=\sqrt{5 – m}x – \sqrt{5 – m}\) là hàm cấp một là:
\(\left\{ \ma trận{ \sqrt {m – 5} \ne 0 \hfill \cr m – 5 \ge 0 \hfill \cr} \ \leftrightarrow \left\{ \ma trận{ m – 5 \ne 0 \hfill \cr m – 5 \ge 0 \hfill \cr} \right.\)
\(\leftrightarrow m – 5 > 0 \leftrightarrow m > 5\)
Vậy \( m > 5\) thì hàm số đã cho là hàm số bậc nhất.
b) Ta có: \(y = \dfrac{m + 1}{m – 1}x +3,5 \rightarrow\) Hệ số \(a =\ dfrac{m + 1}{m – 1}\)
Điều kiện để hàm số \(y = \dfrac{m + 1}{m – 1}x +3,5\) là hàm số bậc nhất là:
\(\left\{ \ma trận{ \dfrac{m + 1}{m – 1} \ne 0 \hfill \cr m – 1 \ne 0 \hfill cr} \right \leftrightarrow \left\{ \ma trận{ m + 1 \ne 0 \hfill \cr m – 1 \ne 0 \hfill \cr} \right . \leftrightarrow \left\{ \ma trận{ m \ne – 1 \hfill \cr m \ne 1 \hfill \cr} \right.\)
Vậy \( m \ne \pm 1\) thì hàm số đã cho là hàm số bậc nhất.
4. Giải bài 14 trang 48 SGK Toán 9 Tập 1
Đối với hàm bậc nhất $y = (1 – \sqrt{5}) x – 1.$
a) Hàm số trên đồng biến hay nghịch biến theo r? Tại sao?
b) Tính giá trị của $y$ khi $x = 1 + \sqrt{5}$
c) Tính giá trị của $x$ khi $y = \sqrt{5}$.
Giải pháp:
a) Ta có:
\(1 < 5 \leftrightarrow \sqrt 1<\sqrt{5}\)
\(\leftrightarrow 1<\sqrt{5}\) \(\leftrightarrow 1-\sqrt{5}<0\)
Vậy hàm \(y = (1 – \sqrt{5}) x – 1\) nghịch biến trên \(\mathbb{r}\) (vì hệ số \(a \) để phủ nhận).
b) Thay \(x = 1 + \sqrt{5}\) vào công thức của hàm đã cho, ta được:
\( y=(1-\sqrt{5})(1+\sqrt{5})-1\)
\(\leftrightarrow y= [1^2 -(\sqrt 5)^2]-1\) \(\leftrightarrow y= (1-5)-1\)
\(\leftrightarrow y= -4-1\) \(\leftrightarrow y= -5\)
Vậy \(x = 1 + \sqrt{5}\) thì \(y= -5\).
c) Ta có:
Thay \(y=\sqrt{5}\) vào công thức của hàm, ta được:
\(\sqrt{5}=(1-\sqrt{5})x-1 \)
\(\leftrightarrow (1-\sqrt 5)x=\sqrt 5 +1\) \(\leftrightarrow x=\dfrac{\sqrt 5 +1}{1- \sqrt 5}\)
\(\leftrightarrow x=\dfrac{(\sqrt 5 +1)(\sqrt 5 +1)}{(1-\sqrt 5)(\sqrt 5 +1)} \)
\(\leftrightarrow x = \dfrac{(\sqrt 5 +1)^2}{(\sqrt 5)^2-1^2}\) \(\leftrightarrow x = \dfrac{(\sqrt 5)^2+2\sqrt 5 +1}{5-1}\)
\(\leftrightarrow x = \dfrac{ 5+2\sqrt 5 +1}{4}\) \(\leftrightarrow x = \dfrac{ 6+2\sqrt 5 }{4}\)
\(\leftrightarrow x = \dfrac{ 2(3+\sqrt 5)}{2.2}\) \(\leftrightarrow x = \dfrac{ 3+\sqrt 5 } {2}\)
Vậy \(y=\sqrt 5\) thì \(x=\dfrac{3+\sqrt 5}{2}\).
Trước:
- Giải bài 8 9 10 trang 48 SGK Toán 9 Tập 1
- Giải bài 15 16 trang 51 SGK Toán 9 Tập 1
- Câu hỏi khác 9
- Học tốt vật lý lớp 9
- Học tốt môn sinh học lớp 9
- Học tốt ngữ văn lớp 9
- Điểm tốt môn lịch sử lớp 9
- Học tốt môn địa lý lớp 9
- Học tốt tiếng Anh lớp 9
- Tiếng Anh lớp 9 thí điểm
- Học Khoa học Máy tính Lớp 9
- Học tốt GDCD lớp 9
Tiếp theo:
Xem thêm:
<3
“Bài tập nào khó, đã có giabaisgk.com”
