Quan hệ giữa các góc trong và các cạnh đối diện của một tam giác: Trả lời câu 1, 2 trang 55; bài 3, 4, 5, 6, 7 trang 56 SGK toán 7 tập 2 – chương 3 hình học 7.
Bài tập 1.So sánh ∠s trong Δabc, ta biết:
ab = 2cm, bc = 4cm, ac = 5cm
Giải pháp: Có trong abc:
ab = 2cm ; BC = 4 cm ; ac = 5cm
⇒ ab <; bc < ca nên ∠c < ∠a <
Bài tập 2.So sánh các cạnh của Δabc, ta biết:
∠a = 800 , b = 450
Giải pháp:
Δabc co a = 800 , b = 450
Vậy ∠c = 1800 – (800 + 450) = 550 (theo định lý tổng ba trong tam giác ∠)
Vì 450 < 550 < 800 hoặc ∠b < c < ∠a < ac ⇒ ac < ab < BC
Xem Thêm: Phun môi 1 tháng chưa lên màu có phải bất thường? Cách khắc phục
Bài 3, trang 56. Đối với Δabc có ∠a = 1000, ∠b = 400
a) Tìm cạnh lớn nhất của .
b) abc là gì?
a) abc co a = 1000 , b = 400
Cạnh lớn nhất của Δabc là bc, vì bc đối với ∠a, ∠a = 1000 > 900 nên a là một tù.
b) ở dạng abc:
∠a + b + c = 1800 (định lý ba tổng của a)
Biết ∠a = 1000; b = 400 (gt)
Thay các số vào: 1000 + 400 + ∠c = 1800 ⇒ ∠c = 400
Vậy b = c = 400
⇒ abc là trọng số tại a.
Bài 4 Trong Δ, góc nào đối diện với cạnh nhỏ nhất (góc, vuông, tù)? Tại sao?
Xem Thêm: Chỉ số RBC trong xét nghiệm máu là gì? Nên xét nghiệm RBC ở đâu?
Trong câu a, cạnh có cạnh nhỏ nhất là góc nhọn, vì nếu là góc vuông hoặc góc tù thì hai s còn lại phải lớn hơn bình phương nên tổng ba s lớn hơn 1800 ( cái này vô nghĩa với tổng của Định lý 3)
Bài 5. Ba bạn Hạnh, Nguyên, Trang đi đến trường theo ba con đường AD, BD, và CD (hình dưới). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng và ∠ACD là ∠tù. Hỏi ai đi xa nhất, ai đi gần nhất? Hãy giải thích 
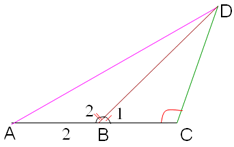
Trong Δdbc, ∠c là ∠tù (gt) ⇒ db > dc (1) và có b1 nhọn.
Ta có b1 + b2 = 1800 (liền kề)
Đó ∠b1<900(cmt)⇒∠b2> 900
Trong Δdab, ∠b2 là ∠tù (cmt) ⇒ da >database (2)
Từ (1) và (2) ta có da >;dB>DC
Cho bạn đi xa hạnh phúc nhất, nơi gần bạn nhất.
Bài 6 trang 56. Xem hình bên, có hai đoạn thẳng bằng nhau là bc và dc. Kết luận nào sau đây là đúng? Tại sao?
a) a = b
b)∠a>;
c)∠a<;
Xem Thêm: Thần chú thu hút tiền bạc là gì và các câu chú cầu tài lộc hiệu quả
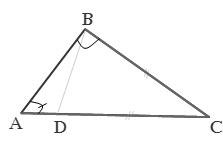
Ta có d nằm giữa a và c (gt) ⇒ ad + dc = ac mà dc = bc (gt) nên ad + bc = ac nên bc <;ac thuộc Δabc ⇒ ∠a < ∠b(Δ Mối quan hệ giữa góc giữa và cạnh đối) Do đó có kết luận c).
Toán 7 trang 56 Bài 7. Cho Δabc và ac >; ab. Trên tia ac lấy điểm b’ sao cho ab’ = ab
a) So sánh abc và abb’
b) So sánh abb’ và ab’b
c) So sánh abb’ và acb
Từ ∠abc>
Giải:a) Vì ac >; ab nên b’ nằm giữa a và c, nên:
∠abc > ab’ (1)
b) abb’ có ab = ab’ nên abb’ là trọng số
Suy ra: abb’ = ab’b (2 )
c) ∠ab’b là góc ngoài tại đỉnh b’ của bb’c nên: ∠ab’b >∠acb
Bốn (1) và (2) ∠abc>
