Bài 5 Trang 12 SGK Hình Học 10
Cho tam giác \(abc\) cạnh \(a\). Tính độ dài của các vectơ \(\overrightarrow{ab}+ \overrightarrow{bc}\) và \(\overrightarrow{ab}- \overrightarrow{bc}\)
NGƯỜI CHIẾN THẮNG
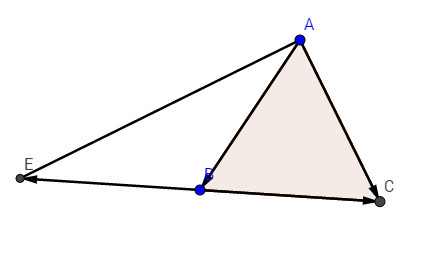
Ta có \(\overrightarrow{ab}+ \overrightarrow{bc}= \overrightarrow{ac}\)
\(\left | \overrightarrow{ab}+\overrightarrow{bc} \right | = \left | \overrightarrow{ac} \right |= a\)
Ta có: \(\overrightarrow{ab} – \overrightarrow{bc} = \overrightarrow{ab} +\overrightarrow{cb}\).
Trên tia \(cb\), ta dựng \(\overrightarrow{be} = \overrightarrow{cb}\)
\( \rightarrow \overrightarrow{ab} – \overrightarrow{bc} = \overrightarrow{ab} +\overrightarrow{be}= \overrightarrow{ae}\)
Tam giác \(eac\) chính xác tại \(a\) (vì trung tuyến \(ab\) bằng một nửa cạnh \(ce\)) với: \( ac = a, ce = 2a\) , kết quả là \(ae = \sqrt {c{e^2} – a{c^2}} = \sqrt {4{a^2} – {a ^ 2 }} = a\sqrt 3 \)
Vì vậy \(\left | \overrightarrow{ab } -\overrightarrow{bc}\right | = \left | \overrightarrow{ae} \right | = a\sqrt3\ )
Bài 6 Trang 12 SGK Hình Học 10
Xem Thêm: Cách vẽ lục giác đều bằng compa và không cần compa đều đẹp
Cho hình bình hành \(abcd\) có tâm \(o\). Bằng chứng:
a) \(\overrightarrow{co} – \overrightarrow{ob} = \overrightarrow{ba}\);
b) \(\overrightarrow{ab} – \overrightarrow{bc} = \overrightarrow{db}\);
c) \(\overrightarrow{da} -\overrightarrow{db} = \overrightarrow{od} – \overrightarrow{oc}\);
d) \(\overrightarrow{da} – \overrightarrow{db} + \overrightarrow{dc} = \overrightarrow{0}\).
NGƯỜI CHIẾN THẮNG
a) Theo quy tắc trừ ba điểm, ta có:
\(\overrightarrow{ba} = \overrightarrow{oa}- \overrightarrow{ob}\) (1)
Mặt khác, \(\overrightarrow{oa} = \overrightarrow{co}\) (2)
Suy ra từ (1) và (2):
\(\overrightarrow{ba} = \overrightarrow{co} – \overrightarrow{ob}\).
b) Ta có: \(\overrightarrow{db}= \overrightarrow{ab} – \overrightarrow{ad}\) (1)
\(\overrightarrow{ad} = \overrightarrow{bc}\) (2)
Xem Thêm: Soạn bài Khúc hát ru những em bé lớn trên lưng mẹ – VietJack.com
Từ (1) và (2) cho ta:
\(\overrightarrow{db} = \overrightarrow{ab}- \overrightarrow{bc}\).
c) Ta có:
\(\overrightarrow{da} – \overrightarrow{db} = \overrightarrow{ba}\) (1)
\(\overrightarrow{od} – \overrightarrow{oc} = \overrightarrow{cd}\) (2)
\(\overrightarrow{ba} = \overrightarrow{cd}\) (3)
Từ (1), (2), (3)
\(\overrightarrow{da} -\overrightarrow{db} = \overrightarrow{od} – \overrightarrow{oc}\) dcm.
d) \(\overrightarrow{da} – \overrightarrow{db} + \overrightarrow{dc} = (\overrightarrow{da} – \overrightarrow{db}) + \overrightarrow{dc }\)
\(= \overrightarrow{ba}+\overrightarrow{dc} = \overrightarrow{ba}+ \overrightarrow{ab}= \overrightarrow{0}\) (vì \( overrightarrow{dc}= \overrightarrow{ab}) \).
Bài 7 Trang 12 SGK Hình Học 10
Đối với \(\overrightarrow{a}\), \(\overrightarrow{b}\) là hai vectơ còn lại \(\overrightarrow{0}\). khi nào có bình đẳng
Xem Thêm: Giải bài tập Toán lớp 5 trang 123 Luyện tập chung – Tailieu.com
a) \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |\) + \ (\left | \overrightarrow{b} \right |\);
b) \(\left | \overrightarrow{a}+\overrightarrow{b} \right |= \left | \overrightarrow{a}-\overrightarrow{b} \right |\).
NGƯỜI CHIẾN THẮNG
a) Ta có \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |\) (\left | \overrightarrow{b} \right |\)
Nếu chúng ta xét hình bình hành \(abcd\) và \(\overrightarrow{ab} = \overrightarrow{dc}= \overrightarrow{a}\) và \(\overrightarrow{ quảng cáo }= \overrightarrow{bc}= \overrightarrow{b}\) thì \(\left | \overrightarrow{a}+\overrightarrow{b} \right |\) là độ dài cặp Góc \(ac\) và \(\left | \overrightarrow{a} \right |= ab\); \(\left | \overrightarrow{b} \right | = bc\).
Ta có: \(ac = ab + bc\)
Bằng nhau khi điểm \(b\) nằm giữa hai điểm \(a, c\).
Vì vậy \(\left | \overrightarrow{a}+\overrightarrow{b} \right | = \left | \overrightarrow{a} \right |+ \left | \ overrightarrow{b} \right |\) khi hai vectơ \(\overrightarrow{a}\), \(\overrightarrow{b}\) cùng hướng.
b) Tương tự, \(\left | \overrightarrow{a}+\overrightarrow{b} \right |\) là độ dài của đường chéo \(ac\)
\(\left | \overrightarrow{a}-\overrightarrow{b} \right |\) là độ dài của đường chéo \(bd\)
\(\left | \overrightarrow{a}+\overrightarrow{b} \right | =\left | \overrightarrow{a}-\overrightarrow{b} \right | ) \(\rightarrow ac = bd\).
Hình bình hành \(abcd\) có hai đường chéo bằng nhau nên là hình chữ nhật, ta có \(ad \perp ab\) hoặc \(\overrightarrow{a} perp\ mũi tên qua phải{b}\).
giaibaitap.me
