Bài tập §3. Hình thang cân, Chương 1 – Hình tứ giác, SGK Toán 8. Bài 16 17 18 19 trang 75 sgk toán 8 tập 1 chứa công thức, lý thuyết và các phương pháp giải toàn diện các bài tập phần hình học trong sách giáo khoa toán, giúp các em học tốt môn Toán lớp 8. .
Lý thuyết
1. định nghĩa
Hình thang cân là hình thang có hai đáy kề bên bằng nhau.
Tứ giác abcd là hình thang cân (đáy ab;cd)
\( \leftrightarrow {\rm{ ab // cd }}\) và \({\rm{\hat c = \hat d}}\)
2. thuộc tính
Định đề 1:Trong hình thang cân, hai cạnh bên bằng nhau.
Định lý 2:Trong hình thang cân, hai đường chéo bằng nhau.
Định lý 3: Hình thang có hai đường chéo bằng nhau là hình thang cân.
3. Logo nhận biết hình thang cân
Hình thang có hai đáy kề nhau là hình thang cân.
Hình thang có hai đường chéo bằng nhau là hình thang cân.
Lưu ý: Hình thang cân có 2 cạnh bên bằng nhau nhưng hình thang có 2 cạnh bên bằng nhau chưa chắc đã là hình thang cân. Ví dụ như hình sau:
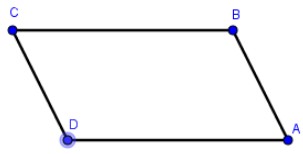
Dưới đây là hướng dẫn giải bài 16, 17, 18, 19 trang 75 SGK Toán 8. Các em đọc kỹ câu hỏi trước khi giải bài nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn lời giải đầy đủ phần bài tập hình học 8 và lời giải chi tiết bài 16 17 18 19 trang 75 SGK toán 8 bài 3. Chương đầu tiên hình thang cân – tứ giác để các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 16 trang 75 SGK Toán 8 tập 1
Tam giác $abc$ cân tại $a$, phân giác $bd, ce$ (d $\in$ ac, e $\in$ ab). Chứng minh rằng $bedc$ là hình thang cân có đáy nhỏ bằng các cạnh bên.
Giải pháp:
Ta có:
$\widehat{abd}$ = $\frac{1}{2}$$\widehat{b}$ (bd là đường phân giác)
$\widehat{ace}$ = $\frac{1}{2}$$\widehat{c}$ (ce là đường phân giác)
$\widehat{b}$ = $\widehat{c}$ (tam giác abc là tam giác cân tại a)
Vậy $\widehat{abd}$ = $\widehat{ace}$
Hãy xem xét hai hình tam giác $adb$ và $aec$:
$\widehat{a}$ trung bình
$ab = ac$(tam giác abc cân tại a)
$\widehat{abd}$ = $\widehat{ace}$ (bằng chứng ở trên)
Vì vậy, $\delta$ adb = $\delta$ aec (g-c-g)
Suy ra $ad = ae$
Vậy tam giác $ade$ cân tại $a$
Ta có:
$\widehat{aed}$ = $\frac{180^0 – \widehat{a}}{2}$ (tam giác ade cân tại a)
$\widehat{b}$ = $\frac{180^0 – \widehat{a}}{2}$ (tam giác cân abc tại a)
Suy ra $\widehat{aed}$ = $\widehat{b}$
Vậy $ed // bc$
Do đó: tứ giác $bedc$ là hình thang
Hình thang $bedc$ có $\widehat{b}$ = $\widehat{c}$ nên $bedc$ là một hình thang cân.
Ta có $ed//bc ⇒ \widehat{d_1} = \widehat{b_2}$ (xen kẽ)
$\widehat{b_1} = \widehat{b_2}$ (bằng chứng ở trên)
Vậy $\widehat{d_1} = \widehat{b_1}$
Tam giác $bed$ do đó cân tại $e$
Suy ra $eb = ed$
Vậy hình thang $bedc$ là một hình thang cân có đáy $ed$ bằng cạnh $eb$.
2. Giải bài 17 trang 75 SGK Toán 8 tập 1
Hình thang $abcd (ab//cd)$ có $\widehat{acd}$ = $\widehat{bdc}$. Chứng minh rằng $abcd$ là hình thang cân.
Giải pháp:
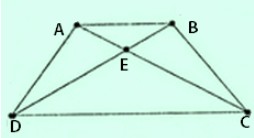
Gọi $e$ là giao điểm của hai đường chéo $ac$ và $bd$
Chúng tôi có
$\widehat{acd}$ = $\widehat{bdc}$ nên tam giác dec là cân tại e
Suy ra $ed = ec(1)$
Ta có: $ab // cd$ ⇒ $\begin{cases}\widehat{acd} = \widehat{bae}\\widehat{bdc} = \widehat{abe } end{case}$
$\widehat{acd} = \widehat{bdc}$ (gt)
Vậy $\widehat{bae} = \widehat{abe}$
Tam giác $aeb$ do đó là tam giác cân tại $a ea = eb(2)$
Được suy ra từ (1) và (2): $ac = bd$
Hình thang $abcd$ có hai đường chéo bằng nhau nên $abcd$ là hình thang cân.
3. Giải bài 18 trang 75 SGK Toán 8 tập 1
Chứng minh định lý “Hình thang có hai đường chéo bằng nhau là hình thang cân” bằng cách đặt câu hỏi sau: Cho hình thang $abcd (ab//cd)$ có $ac = bd$. Vẽ một đường thẳng song song với $ac$ qua b, cắt đường thẳng $dc$ tại $e$. Bằng chứng:
a) $\delta bde$ là tam giác cân
b) $\delta acd = \delta bdc$.
c) hình thang $abcd$ là hình thang cân
Giải pháp:
a)Chúng tôi có
$ab//cd$⇒ $\begin{cases}ab//ce\\ac//be\end{cases}$
$ ⇒ ac = be$
Ta lại có: $ac = bd (gt) be = bd$
Tam giác $bde$ do đó là tam giác cân tại $b$.
b) Ta có $ac//be$ ⇒ $\widehat{acd} = \widehat{bec}$ (hai góc đồng vị)
Ta có:
$\widehat{bde} = \widehat{bec}$ (tam giác bde là tam giác cân tại b)
⇒ $\widehat{bdc} = \widehat{acd}$
Hãy xem xét hai hình tam giác $acd$ và $bdc$:
bên cạnh $dc$ bình thường
$\widehat{bdc} = \widehat{acd}$ (bằng chứng ở trên)
$ad = bd (gt)$
Vậy $\delta acd = \delta bdc (c-g-c)$
c) Hình thang $abcd$ có:
$\widehat{adc} = \widehat{bcd}$ ($\delta acd = \delta bdc$)
Vậy hình thang $abcd$ là hình thang cân.
4. Giải bài 19 trang 75 SGK Toán 8 tập 1
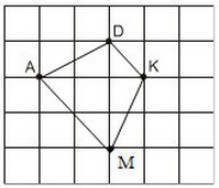
Đố vui. Cho ba điểm $a, d, k$ trên tờ giấy hình vuông (h.32). Tìm giao điểm của điểm thứ tư $m$ với đường thẳng gồm ba điểm đã cho là bốn điểm của hình thang cân.
Giải pháp:
Nếu mỗi hình vuông có cạnh dài $1$ đơn vị thì:
Ta có: $ak = 3$ nên phải chọn $m$ sao cho $am//dk$ và $dm = 3$. Sau đó, chúng tôi nhận được một hình thang cân $adkm$ như hình dưới đây.
Trước:
- Giải bài 11 12 13 14 15 Trang 74 75 SGK Toán 8 Tập 1
- Giải bài 20 21 22 23 24 25 trang 79 80 SGK Toán 8 Tập 1
- Câu hỏi khác 8
- Học tốt vật lý lớp 8
- Học tốt môn sinh học lớp 8
- Học tốt ngữ văn lớp 8
- Điểm tốt môn lịch sử lớp 8
- Học tốt môn địa lý lớp 8
- Học tốt tiếng Anh lớp 8
- Học tốt môn tiếng Anh lớp 8 thí điểm
- Học Khoa học Máy tính Lớp 8
- Học chăm chỉ môn gdcd lớp 8
Tiếp theo:
Xem thêm:
<3
“Môn thể thao nào đã khó giabaisgk.com”
