Bài 6 Trang 109 – SGK Toán 7 Tập 1
Tìm số đo \(x\) trong hình bên dưới:
Người chiến thắng:
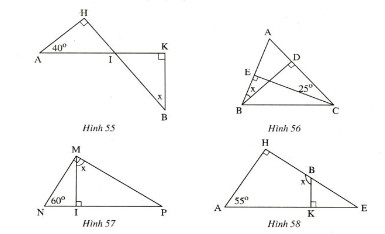
Hình 55)
Theo định lý tổng hai góc nhọn của một tam giác vuông thì bù nhau, ta áp dụng cho \(\delta ahi\,\text{have}\,\widehat h = { 90^0} ) Ta có:
\(\widehat{a}+\widehat{aih}= 90^0\), (1)
Áp dụng cho \(\delta bki\,\text{ và }\,\widehat k = {90^0}\) ta được:
\(\widehat{b}\) + \(\widehat{bik} = 90^0\) (2)
Vậy \(\widehat{aih}\)= \(\widehat{bik}\) (vì hai góc đối đỉnh) (3)
Từ (1), (2) và (3) suy ra \(\widehat{a}\) = \(\widehat{b}\)
Vậy \(\widehat{b}=x= 40^0\)
Đợt 56)
Theo định lý tổng hai góc nhọn của một tam giác vuông bù nhau, ta áp dụng cho \(\delta abd\,\text{have}\,\widehat {adb} = { 90^ 0 }\) ta có:
\(\widehat{abd}\) +\(\widehat{a}= 90^0\), (1)
Áp dụng cho \(\delta ace\,\text{ }\,\widehat {aec} = {90^0}\) ta được:
\(\widehat{ace}\)+ \(\widehat{a}=90^0\), (2)
Từ (1) và (2) suy ra \(\widehat{ace}\) = \(\widehat{abd}=25^0\)
Vậy\(x=25^0\)
Dụ ngôn 57)
Ta có: \(\widehat{nmp}=\widehat{nmi}\) + \(\widehat{pmi}= 90^0\), (1)
Theo định lý tổng hai góc nhọn của một tam giác vuông bù nhau ta áp dụng cho \(\delta mni\,\text{have}\,\widehat {min} = {90^ 0 }\) ta có:
\(\widehat{n }\) + \(\widehat{nmi}= 90^0\), (2)
Từ (1) và (2) suy ra \(\widehat{n }\) = \(\widehat{pmi}=60^0\)
Vậy\(x=60^0\)
Hình 58)
Theo định lý tổng hai góc nhọn của một tam giác vuông thì bù nhau, ta áp dụng cho \(\delta ahe\,\text{有}\,\widehat {ahe } = {90^ 0 }\) ta có:
\(\widehat{e }\) + \(\widehat{a}=90^0\)
\(\widehat{e }= 90^0- \widehat{a} = 90^0- 55^0= 35^0\)
\(\widehat{kbh }=\widehat{bke}+ \widehat{e }\) (góc ngoài của tam giác\(bke\))
\(= 90^0+ 35^0= 125^0\)
Vậy\(x=125^0\)
Bài 7 Trang 109 – SGK Toán 7 Tập 1
Tam giác \(abc\) tại \(a\). Đường thẳng \(ah\) vuông góc với \(bc\) (\(h\) nằm trên \(bc\)).
a) Tìm các cặp góc bù nhau trong hình bên.
b) Tìm các cặp góc nhọn bằng nhau trong hình vẽ.
NGƯỜI CHIẾN THẮNG
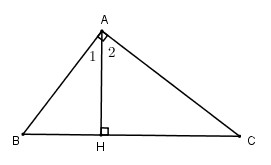
a) Tam giác \(abc\) nằm trong \(a\) nên \(\widehat{b }\) + \(\widehat{c }= 90^ 0 )
Hoặc \(\widehat{b }\), \(\widehat{c }\) lẫn nhau,
Tam giác \(ahb\) vuông tại \(h\) nên \(\widehat{b }\)+ \(\widehat{a_{1} }= 90 ^ 0 \)
Hoặc \(\widehat{b }\), \(\widehat{a_{1} }\) lẫn nhau.
Tam giác \(ahc\) vuông tại \(h\) nên \(\widehat{a_{2} }\)+ \(\widehat{c } = 90 ^ 0\)
Hoặc \(\widehat{a_{2} }\), \(\widehat{c }\) lẫn nhau.
hai)
Ta có \(\widehat{b }\) + \(\widehat{c }= 90^0\)
\(\widehat{b }\)+ \(\widehat{a_{1} }= 90^0\)
\(\rightarrow \widehat{a_{1} }=\widehat{c }\)
\(\widehat{b }\) + \(\widehat{c }=90^0\) và \(\widehat{a_{2} }\)+ (\widehat{c }\) = \(90^0\)
\(\rightarrow \widehat{a_{2} }\) = \(\widehat{b }\)
Bài 8 Trang 109 – SGK Toán 7 Tập 1
Đối với tam giác \(abc\) có \(\widehat{b}=\widehat{c}= 40^0\). Gọi \(ax\) là tia phân giác của góc ngoài tại đỉnh \(a\), chứng minh \(ax// bc\).
NGƯỜI CHIẾN THẮNG
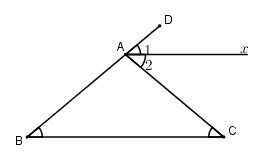
\(\widehat{cad}\) = \(\widehat{b}\)+ \(\widehat{c}\) (góc ngoài của tam giác\( abc ))
\(= 40^0\)+ \(40^0\) = \(80^0\)
\(\widehat{a_{2} }= \frac{1}2\widehat{cad}=\frac{80}2=40^0\)
\(a_2=\widehat{bca }\) hai góc so le trong thì bằng nhau nên \(ax// bc\)
Bài 9 Trang 109 – SGK Toán 7 Tập 1
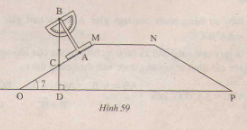
Hình 59 là mặt cắt ngang của đê, dùng thước \(t\) đo góc nhọn \(mop\) tạo bởi mái dốc của đê và mặt phẳng nằm ngang, rồi đặt nó để hiển thị (\(oa\perp ab\ )). Tính góc \(mop\), biết dây dọi \(bc\) và trục \(ba\) \(\widehat{abc }= 32^0 )
Người chiến thắng:
Ta có tam giác vuông \(abc\) tại \(a\) nên
\(\widehat{abc}+ \widehat{acb}= 90^0\) (1)
Tam giác \(ocd\) ở bên phải của \(d\) có \(\widehat{mop}= \widehat{ocd}= 90^0\) (2)
Ngược lại: \( \widehat{acb}=\widehat{ocd}\) (hai đường chéo) (3)
Được suy ra từ (1), (2), (3): \(\widehat{mop}= \widehat{abc}=32^0\)
giaibaitap.me
