Tìm bài toán nghịch đảo các thành phần r, l, c của một đoạn mạch điện xoay chiều là dạng bài khó tổng hợp nhiều kiến thức. Vì vậy bạn đọc phải nắm chắc về phương trình u, i, giản đồ véc tơ, hiện tượng cộng hưởng, độ lệch pha, v.v….
Bài toán nghịch đảo rlc đã xác định
Tínhtổng trở z,điện trở r-điện cảm zl-điện dung zc-điện cảm l và điện dung c
1. Phương pháp chung:
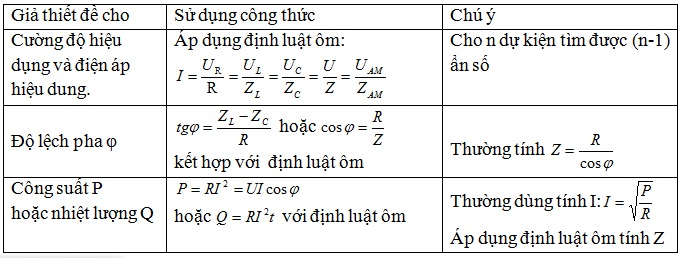
+Nhớ công thức ôm, công thức tính trở kháng….:
– Biết bạn và tôi: z=u/i
– Biết zl, zc và r: \(z=\sqrt{r^{2}+(z_{l}-z_{c})^{2}}\):\(z_ {l}=\omega l,z_{c}=\frac{1}{\omega c}\), trong đó đơn vị của l là (h) và đơn vị của c là (f)
– biết r và j hoặc cosj : z=r/cosφ
Nếu cuộn cảm có điện trở hoạt động r, thì mạch rlrc sẽ có điện trở thuần tương đương là r+r; khi đó \(z=\sqrt{(r+r)^{2}+(z_{ l }-z_{c})^{2}}\)
+Công thức kháng r:
– Nếu biết l, c và φ: Công thức tính: \(tan\varphi =\frac{z_{l}-z_{c}}{r}\) ; nếu điện trở của cuộn cảm Đối với r: \(tan\varphi =\frac{z_{l}-z_{c}}{r+r}\)
– Biết z và φ hoặc cosφ : r= z.cosφ;nếu cuộn cảm có điện trở r:\(cos\varphi =\frac{r+r}{z}\)
– biết p và i:\(p=ri^{2}\) ; nếu cuộn cảm có điện trở r: công suất mạch: p=(r+r)i2
+Công thức của độ tự cảm zl và điện dung zc: \(z_{l}=\omega l=2\pi fl;z_{c}=\frac{1} { \omega c}=\frac{1}{2\pi fc}\) ;
– Biết z và r, hãy tính hiệu: \((z_{l}-z_{c})=\pm \sqrt{z^{2}-r^{2}}\) Khi biết zc thì tính zl, ngược lại thì tính l và c
-Lưu ý bổ sung: \(z_{l}.z_{c}=\frac{l}{c}\); Cộng hưởng điện : zl= zc hoặc:\ (\omega ^{2}lc=1\) hoặc \(\omega =\frac{1}{\sqrt { lc}}\)
-Khi vấn đề là điện áp hiệu dụng giữa các thành phần và mạch điện, công suất tiêu tán chứ không phải dòng điện, thì hãy sử dụng điện áp hiệu dụng cho phương trình.
– Khi tìm thấy ur, nó sẽ tìm \(i=\frac{p}{u_{r}}\) rồi tìm \(r=\frac{u_{r}} {i}; z_{l}=\frac{u_{l}}{i};z_{c}=\frac{u_{c}}{i}\)
– Mức tiêu thụ năng lượng: \(p=u.i.cos\varphi =i^{2}r=\frac{u^{2}r}{z^{2}}\) ; hoặc \ (p=\frac{u^{2}r}{r^{2}+(z_{l}-z_{c})^{2}}\) hoặc p= uri
– Hệ số công suất\(k=cos\varphi =\frac{r}{z}=\frac{p}{ui}=\frac{u_{r}}{u} \ )
– Nhiệt lượng tỏa ra trên đoạn mạch (tại r): q = ri2t (đơn vị t: s, đơn vị q: j)
– Ngoài ra cần quan tâm đến giản đồ vector để vẽ mạch này cho đảm bảo phương trình không sai số.
2. Ví dụ 1:
+Ví dụ 1: Tính điện trở toàn phần của đoạn mạch sau:
A. Cho mạch điện không phân nhánh rlc: uc = 4v; u = 16v; ul = 20v; i = 2a
Mạch rl mắc nối tiếp với r=20Ω, u và i lệch pha nhau 60o
Cho đoạn mạch rc nối tiếp có r=10Ω; u và i lệch pha nhau 30o
d là mạch điện rlc nối tiếp có r=60Ω; hệ số công suất 0,6
NGƯỜI CHIẾN THẮNG:
a. Vì i và uc;ur,ul nên dùng công thức:
Xem Thêm: Cách tính múi giờ và điều thú vị về múi giờ trên trái đất – CMMB
r = ur/i = 16/2 = 8Ω; zl= ul/i = 20/2=10Ω; zc= uc/i = 4/2=2Ω;
Suy luận: z= \(\sqrt{8^{2}+(10-2)^{2}}=8\sqrt{2}\omega\)
b.Vì: r = 20 Ω;φ = \(\frac{\pi }{3}\) Nên ta có: tan φ = \(\frac{z_{l}} {r}\) => zl = r. tan =20\(\sqrt{3}\) .
Vì chủ ngữ cho: r = 10 Ω; φ =\(-\frac{\pi }{6}\) Nên ta có: tan φ = \(-\frac{ z_{ c}}{r}\) => zc = -r. tan φ=10\(\frac{\sqrt{3}}{3}\) Ω.
Vì đề cho: r = 60 Ω; cosφ = 0.6 mà cosφ =\(\frac{r}{z}\) => z =\(\frac{r}{ cos varphi }\) = 60/ 0,6 = 100 Ω.
+Ví dụ 2: Như hình bên là mạch điện xoay chiều. uab=hằng số; f=50(hz), có thể bỏ qua điện trở của nút k và ampe kế. \(c=\frac{10^{-4}}{\pi }(f)\). Khi chuyển khóa k từ vị trí 1 sang vị trí 2 thì số chỉ của ampe kế không thay đổi. Tính độ tự cảm l của cuộn dây?
A. \(\frac{10^{-2}}{\pi }(h)\) b.\(\frac{10^{-1}}{\pi }(h) ) c. \(\frac{1}{\pi }(h)\) d.\(\frac{10}{\pi }(h)\)
Giải pháp:\(z_{c}=100\omega ;\omega =100\pi (rad/s)\)
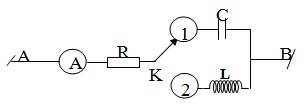
Khi khóa k ở vị trí 1, đoạn mạch gồm hai phần tử r và c.
Vậy ta có: \(i=\frac{u_{ab}}{z_{ab}}=\frac{u_{ab}}{\sqrt{r^{2}+{z_ {c}}^{2}}}(1)\)
Khi khóa k ở vị trí số 2 thì mạch điện gồm hai phần tử r và l:
Vậy ta có: \(i’=\frac{u_{ab}}{z’_{ab}}=\frac{u_{ab}}{\sqrt{ r^{2}+{z_{l}}^{2}}}(2)\)
Theo chủ đề i=i’ nên (1) = (2) :\(\frac{u_{ab}}{\sqrt{r^{2}+{z_{c} } ^{2}}}=\frac{u_{ab}}{\sqrt{r^{2}+{z_{l}}^{2}}}\)
Suy luận: \(\frac{1}{\sqrt{r^{2}+{z_{c}}^{2}}}=\frac{1}{ sqrt{r^{2}+{z_{l}}^{2}}}\rightarrow \sqrt{r^{2}+{z_{c}}^{2}}=\sqrt{ r ^{2}+{z_{l}}^{2}}\)
\(\rightarrow z_{l}=z_{c}=100\omega \rightarrow l=\frac{z_{l}}{\omega }=\frac{ 100}{100\pi }=\frac{1}{\pi }(h)\)
+Ví dụ 3 : Cho mạch điện như hình vẽ: u= \(120\sqrt{2}cos(100\pi t) ) (năm); cuộn dây có r = 15Ω; \(l=\frac{2}{25\pi }(h)\). c là tụ điện thay đổi được. Điện trở vôn kế rất cao. Điều chỉnh c để số chỉ của vôn kế lớn nhất. Tìm c và số chỉ vôn kế lúc này?
a.\(c=\frac{10^{-2}}{8\pi }(f);u_{v}=136(v)\) b.\(c= \frac{10^{-2}}{4\pi }(f);u_{v}=163(v)\)
c.\(c=\frac{10^{-2}}{3\pi }(f);u_{v}=136(v)\) d.\(c= \frac{10^{-2}}{5\pi }(f);u_{v}=186(v)\)
Giải:Vì vôn kế được mắc vào cả hai đầu cuộn dây nên số chỉ của vôn kế là:
\(u_{v}=u_{d}=i.z_{d}=\frac{u}{z}.z_{d}=\frac{u}{\sqrt{r ^{2}+(z_{l}-z_{c})^{2}}}.\sqrt{r^{2}+(\omega l)^{2}}\)
Vì zd không phụ thuộc vào c nên nó không đổi. Vì vậy, biểu thức cho tử số vẫn giữ nguyên.
=>Số chỉ vôn kế lớn nhất khi mẫu số nhỏ nhất: \((\sqrt{r^{2}+(z_{l}-z_{c})^{2}}) _{ phút} \)
Điều này xảy ra khi là cộng hưởng điện: \(z_{c}=z_{l}=8(\omega )\) .
Suy luận: \(c=\frac{10^{-2}}{8\pi }(f)\), thì z = r
Và số chỉ của vôn kế: \(u_{v}=u_{d}=\frac{u}{r}.\sqrt{r^{2}+(\omega l ) ^ {2}}=\frac{120}{15}.\sqrt{15^{2}+(8)^{2}}=\frac{120}{15}.17=136v )
Chọn một.
+Ví dụ 4: Một mạch điện xoay chiều gồm cuộn dây có điện trở r = 30w, độ tự cảm h mắc nối tiếp với tụ điện thành tụ điện c.Điện áp tức thời trên đoạn mạch là: (v). Khi chọn c thì công suất tiêu thụ của đoạn mạch là bao nhiêu và công suất cực đại là bao nhiêu?
A. \(c=\frac{10^{-4}}{2\pi }\)f và \(p_{max}=120\)w. b. \(c=\frac{10^{-4}}{\pi }\)f và \(p_{max}=120\sqrt{2}\)w.
\(c=\frac{10^{-3}}{4\pi }\)f và \(p_{max}=240\)w. d. \(c=\frac{10^{-3}}{\pi }\)f và \(p_{max}=240\sqrt{2}\)w.
Xem Thêm: Mẫu hợp đồng thiết kế kiến trúc thông dụng, phổ biến
Giải pháp: Sức mạnh: \(p=i^{2}r=\frac{u^{2}r}{r^{2}+(z_{l} – z_{c})^{2}}\) Ta có pmax \(z_{l}=z_{c})^{2}\leftrightarrow \frac{1}{\omega c }=\omega l\)
\(c=\frac{1}{\omega^{2} l}=\frac{1}{(100\pi )^{2}.\frac{0,4 }{\pi }}=\frac{10^{-3}}{4\pi }f\rightarrow p_{max}=\frac{u^{2}}{r}=\ Điểm {120^{2}}{2.30}=240w\)
Chọn c.
+Ví dụ 5: đối với mạch không phân nhánh. r=100Ω, cuộn cảm l=0,318h, f=50hz, điện dung thay đổi. Đặt một điện áp xoay chiều có giá trị bình phương trung bình gốc là \(u=100\sqrt{2}\)v trên toàn mạch. Điều chỉnh c để mạch có cộng hưởng điện. Giá trị c và cường độ dòng điện khi đó là:
A. c = 31,8mf và i = \(\sqrt{2}\)a. b.c = 31,8mf và i=2\(\sqrt{2}\)a.
c = 3,18mf và i = 3\(\sqrt{2}\) d. c = 63,6mf và i = 2a.
Giải: Độ tự cảm: \(z^{l}=2\pi fl=2\pi .50.0.318=100\omega\); khi zc = zl = 100Ω thì mạch có cộng hưởng.
\(\rightarrow c=\frac{1}{2\pi f.z_{c}}=\frac{1}{2\pi .50.100}=\frac{10 ^{-4}}{\pi }f=31.8\mu f;\)\(i_{max}=\frac{u}{r}=\frac{100\sqrt {2 }}{100}=\sqrt{2}a\)
Chọn một.
+Ví dụ 6: Cho đoạn mạch gồm r, l, c mắc nối tiếp. r thay đổi \(l=\frac{1}{\pi }h,c=\frac{10^{-3}}{4\pi }f\) để đặt điện áp xoay chiều qua mạch \(u=75\sqrt{2}cos100\pi t(v)\). Công suất của toàn mạch là p = 45w. Giá trị của điện trở r là bao nhiêu?
A. r = 45Ω b. r = 60Ω c. r = 80Ω câu a hoặc câu c
NGƯỜI CHIẾN THẮNG:
Mức tiêu thụ năng lượng:
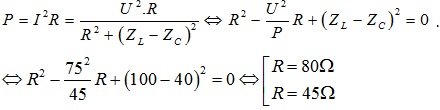
Chọn d.
+Ví dụ 7: Đoạn mạch gồm điện trở thuần r = 100Ω và tụ điện có điện dung c mắc nối tiếp. Biết biểu thức của hiệu điện thế u = 100 cos100πt v ở hai đầu đoạn mạch và cường độ sáng hiệu dụng i = 0,5 a trong mạch. Tính tổng trở của đoạn mạch và điện dung của tụ điện?
A. z=100\(\sqrt{2}\)Ω ; c=\(\frac{1}{\omega z_{c}}=\frac{1}{\pi }. 10^{-4}f\) b. . z=200\(\sqrt{2}\)Ω ; c= \(\frac{1}{\omega z_{c}} =\frac{1}{\pi }.10^{-4}f\)
z=50\(\sqrt{2}\)Ω ; c=\(\frac{1}{\omega z_{c}}=\frac{1}{\ pi }.10^{-4}f\) d. . z=100\(\sqrt{2}\)Ω ; c= \(\frac{1}{\omega z_{ c}}=\frac{1}{\pi }.10^{-3}f\)
hd Cách giải quyết: Chọn một. dl hug z= u/i =100\(\sqrt{2}\)Ω ; sử dụng công thức z =\(z=\sqrt{r^{2}+{z_{ c }}^{2}}=\sqrt{100^{2}+{z_{c}}^{2}}\)
Suy ra \(z_{c}=\sqrt{z^{2}-r^{2}}=\sqrt{2.100^{2}-100^{2}}=100\ omega \) ;c=\(\frac{1}{\omega z_{c}}=\frac{1}{\pi }.10^{-4}f\)
+Ví dụ 8:
Mạch điện xoay chiều Abdef bao gồm các thành phần sau mắc nối tiếp (xem hình)
– Một cuộn dây thuần cảm có độ tự cảm l.
– Hai điện trở giống nhau, mỗi điện trở có giá trị r.
– Tụ điện có điện dung c.
Nối một điện áp xoay chiều có giá trị hiệu dụng uaf=50v và tần số f=50hz vào hai đầu đoạn mạch a và f. Hiệu điện thế trên đoạn mạch đã thử là uad=40v, ube=30v và cường độ dòng điện hiệu dụng trong mạch là i = 1a
a) Tính các giá trị r, l và c
b) Tính hệ số công suất của đoạn mạch
c) Tính độ lệch pha giữa các điện áp uad và udf.
Khoa Tài chính Kế toán – 1999
Xem Thêm: Quy tắc nhấn trọng âm trong tiếng Anh
Giải phápa) Trở kháng
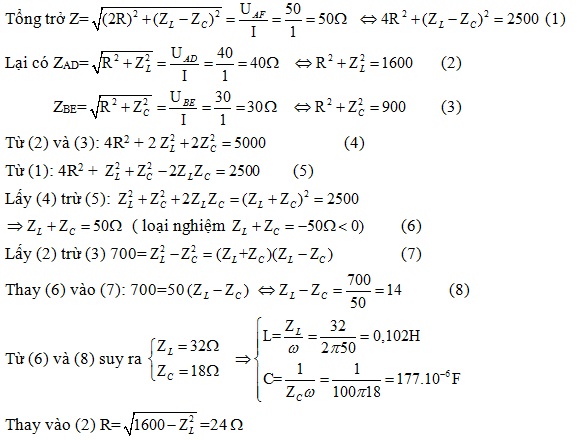
b) Hệ số công suất\(cos\varphi =\frac{2r}{z}=\frac{2.24}{50}=0.96\)
c) uad sớm pha hơn i là φ1 và tanφ1= \(-\frac{z_{c}}{r}=\frac{3}{4}\);
Giai đoạn udf sớm hơn i là φ2, trong đó tanφ2=\(\frac{z_{l}}{r}=\frac{4}{3}\)
Ta có tanφ1. tanφ2= – 1 có nghĩa là uad \(\frac{\pi }{2}\) sớm hơn udf.
+Ví dụ 9: Một mạch điện xoay chiều gồm điện trở thuần r, cuộn dây thuần cảm có độ tự cảm l và tụ điện có điện dung c mắc nối tiếp. Đặt một điện áp xoay chiều u có tần số 1000hz vào hai đầu đoạn mạch. Khi mắc ampe kế a có điện trở không đáng kể song song với tụ điện c thì nó chỉ 0,1A. Cường độ dòng điện qua nó lệch pha π/6 rad so với điện áp trên đoạn mạch góc. Thay ampe kế a bằng vôn kế v có điện trở lớn thì vôn kế chỉ 20v và điện áp trên vôn kế chậm pha π/6rad so với điện áp trên mạch. Giá trị của độ tự cảm l và điện trở thuần r như sau:
Cách khắc phục:* Mắc song song với ampe kế nên chập tụ điện => mạch chỉ có r, l. i1=0,1a – độ lệch pha: φ1 = π/6 => \(r=\sqrt{3}z_{l}\) (1). – chúng ta có: \(u=i.z=0.1.\sqrt{r^{2}+{z_{l}}^{2}}=0.1.\sqrt{r^{2} +\frac {r^{2}}{3}}=0.1.\sqrt{\frac{4r^{2}}{3}}=0.2\frac{r}{ sqrt{3}}\ )(2) *Nối vôn kế với c, uc=20v thì mạch có r, l, c. – chúng ta có uc \(\sqrt{3}r=z_{c}-z_{l}\) chậm hơn u /6 rad => φ2 = -π/3 => .
\(\rightarrow z=2r\) . Do u máu không nguyên vẹn => \(i=\frac{u}{z}=\frac{0,2r}{\sqrt{3}.2r}=\frac{0,1} { sqrt{3}} \) – ta có: \(z_{c}=\frac{u_{c}}{i}=\frac{20}{\frac{0,1 }{ \sqrt{3} }}=200\sqrt{3}\omega\)
– lấy (3) chia (1) và biến đổi ta có: \(z_{l}=\frac{z_{c}}{4}=\frac{200\sqrt{3} } {4}=50\sqrt{3}\omega\)
\(\rightarrow z_{l}=2\pi fl\rightarrow l=\frac{z_{l}}{2\pi f}=\frac{50\sqrt{ 3}}{200\pi }=\frac{\sqrt{3}}{40\pi }(h)\) – từ (1) ta được .\(r=\sqrt { 3}z_{l}=\sqrt{3}.50\sqrt{3}=150\omega\)
Nhiều: a
3. Trắc nghiệm:
câu1.Đoạn mạch xoay chiều gồm cuộn dây thuần cảm và điện trở thuần mắc nối tiếp. So với cường độ dòng điện trong đoạn mạch, hiệu điện thế ở hai đầu đoạn mạch \(\frac{\pi }{3}\) và u = 160v, i = 2a; giá trị điện trở thuần là:
a.80\(\sqrt{3}\) Ω b.80 Ω c.40\(\sqrt{3}\)Ω d. 40
Câu 2: Một cuộn dây được mắc vào nguồn điện xoay chiều u = 200cos(100π t- π/2) (v) thì cường độ dòng điện chạy qua cuộn dây là: i = \ (\ sqrt{2 }\) cos (100πt – \(\frac{5\pi }{6}\)). Độ tự cảm của cuộn dây là:
A. l = \(\frac{\sqrt{2}}{\pi }\) h b. l = \(\frac{1}{\pi }\) h c. l = \(\frac{\sqrt{6}}{2\pi }\) h đ. l = \(\frac{2}{\pi }\) h
câu3. Cho mạch điện xoay chiều rlc không phân nhánh và ampe kế để đo cường độ dòng điện trong mạch. Cuộn dây với \(r=10\omega ,l=\frac{1}{10\pi }h\), mắc thêm một dao động điều hòa có bình phương trung bình u = 50 ở hai đầu đoạn mạch v và tần số f = 50 Hz. Khi dung lượng của tụ điện là c1 thì ampe kế chỉ giá trị cực đại bằng 1a. Giá trị của r và c1 là a. r=40Ω và \(c_{1}=\frac{10^{-3}}{\pi }f\) b.r=50Ω và \(c_{1}=\frac{2.10^ {-3}}{\pi }f\) c. r=40Ω và \(c_{1}=\frac{2.10^{-3}}{\pi }f\) d. r=50Ω và \(c_{1}=\frac{10^{-3}}{\pi }f\)
Câu 4. Cho mạch điện xoay chiều ab gồm điện trở thuần r mắc nối tiếp với cuộn dây thuần cảm l. Khi tần số dòng điện bằng 100hz thì điện áp hiệu dụng ur = 10v, uab = 20v và cường độ dòng điện hiệu dụng qua mạch là i = 0,1a. r và l lần lượt có giá trị nào sau đây?
A. r = 100Ω; l = \(\sqrt{3}\) /(2π) h. b.r = 100Ω;l = \(\sqrt{3}\) /π h.
r = 200Ω ; l = 2/π h. d. r = 200Ω; l =\(\sqrt{3}\) /π h.
Câu 5: Đoạn mạch rlc mắc nối tiếp, khi tần số dòng điện là f thì cuộn cảm zl=25(Ω), khi tần số đoạn mạch là f0 thì điện dung zc=75( Ω) thì cường độ dòng điện trong mạch đạt giá trị cực đại. Kết luận nào sau đây là đúng:
A. f0 = \(\sqrt{3}\)f b. f =\(\sqrt{3}\) f0 c. f0 = 25\(\sqrt{3}\)f d. f = 25\(\sqrt{3}\)f0
Câu 6: Một đoạn mạch gồm điện trở r và cuộn dây thuần cảm l mắc nối tiếp, l thay đổi được. Điện áp hiệu dụng trên mạch là u và tần số góc ω=200(rad/s). Độ lệch pha của u đối với i là φ1 khi l = l1 = π/4(h) và độ lệch pha của u là φ2 khi l = l2 = 1/π(h). Biết rằng 1+2=900. Giá trị của điện trở r là
A. 50Ω. b.65Ω. c. 80Ω. mất 100Ω.
hd: Sử dụng công thức: tanφ1 + tanφ2 = sin(φ1 + φ2 )/ (cos φ1 .cos φ2 )
Câu7 (cĐ 2007): Giả sử điện áp xoay chiều u = 5\(\sqrt{2} \)cos (ωt) Hai đầu mỗi phần tử không đổi: điện trở thuần r, cuộn dây thuần cảm có độ tự cảm l, tụ điện có điện dung c, cường độ dòng điện hiệu dụng qua mỗi phần tử là 50ma. Đặt hiệu điện thế này vào hai đầu đoạn mạch gồm các linh kiện trên mắc nối tiếp thì tổng trở của đoạn mạch là
A. 3100Ω. b.100 yên. c. 2100Ω. mất 300 yên.
Tất cả nội dung bài viết. Vui lòng xem thêm và tải về các tài liệu chi tiết sau:
Tải xuống
Bài tập trắc nghiệm Vật Lý lớp 12 – Xem ngay


