Bóng-bóng-bóng là gì? Công thức giải nhanh, thể tích, vị trí tương đối
1. mặt cầu
Tập hợp các điểm trong không gian cách một điểm cố định $o$ một khoảng $r$ được gọi là hình cầu có tâm $o$ và bán kính $r$. Ký hiệu: $s\left( o;r \right)=\left\{ m\left| om=r \right. \to\}.$
2. hình cầu
Hình cầu $s\left( o;r \right)$ và các điểm bên trong nó được gọi là hình cầu, có tâm $o$ và bán kính $r$. Ký hiệu: $b\left( o;r \right)=\left\{ m\left| om\le r \right. \to\}.$
Nếu $oa,ob$ là hai bán kính của một mặt cầu sao cho $a,o,b$ thẳng hàng thì đoạn thẳng $ab$ được gọi là đường kính của mặt cầu.
Lý thuyết: Cho các điểm a, b cố định. Tập hợp các điểm m trong không gian sao cho $\widehat{amb}={{90}^{0}}$ là hình cầu có đường kính ab.
+ $a\in s\left( o;r \right)\leftrightarrow oa=r.$
+ $o{{a}_{1}}<r\leftrightarrow {{a}_{1}}$ bên trong hình cầu.
+ $o{{a}_{2}}>r\leftrightarrow {{a}_{2}}$ nằm ngoài hình cầu.
3. Khối đa diện ngoại tiếp hình cầu
Định nghĩa: Mặt cầu đi qua mỗi đỉnh của khối đa diện $\left( h \right)$ được gọi là khối đa diện ngoại tiếp $\left( h \right) của khối cầu )$ thì $\left( h \right)$ được cho là khắc trên quả cầu.
Điều kiện cần và đủ để một hình chóp có mặt cầu ngoại tiếp là đáy của nó là một đa giác nội tiếp trong một đường tròn.
Mỗi tứ diện có một mặt cầu ngoại tiếp.
4. Khối đa diện ngoại tiếp hình cầu
A. Mặt cầu nội tiếp hình chóp là mặt cầu nằm bên trong hình chóp và tiếp xúc với tất cả các mặt của hình chóp.
Tâm của mặt cầu khoét thành hình chóp cách đều tất cả các mặt của hình chóp.
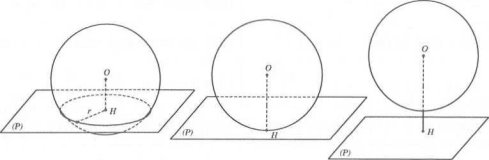
5. Vị trí tương đối của mặt cầu và mặt phẳng
Cho hình cầu $s\left( o;r \right)$ và mặt phẳng $\left( p \right)$, gọi d là khoảng cách từ o đến $\left( p right) distance)$ và h là các hình chiếu đứng của o trên $\left( p \right)$. sau đó
+ if $d<r$ then mặt phẳng (p) cắt mặt cầu $s\left( o;r \right)$ bởi giao tuyến là đường tròn nằm trên mặt phẳng $\left( p right)$ có Với h là tâm, bán kính là $r=\sqrt{{{r}^{2}}-{{d}^{2}}}.$
Khi $d=0$ thì mặt phẳng (p) đi qua tâm o của mặt cầu gọi là mặt phẳng thủy tinh, giao điểm của mặt phẳng thủy tinh và mặt cầu là đường tròn tâm o, bán kính r, gọi là đường tròn lớn của mặt cầu .
+ Nếu $d=r$ thì mặt phẳng $\left( p \right)$ và mặt cầu $s\left( o;r \right)$ có một điểm chung là h.
Sau đó, chúng tôi nói rằng $\left( p \right)$ chạm vào $s\left( o;r \right)$ tại h và cuộc gọi $\left( p \right)$ là tiếp tuyến h của mặt cầu gọi là tiếp tuyến.
Chú ý. Cho h là hình cầu $s\left( o;r \right)$ và mặt phẳng $\left( p \right)$ đi qua h . Sau đó, $\left( p \right)$ và $s\left( o;r \right)\leftrightarrow oh\bot \left( p \right).$
+ Nếu $d>r$ thì mặt phẳng $\left( p \right)$ và hình cầu $s\left( o;r \right)$ không có điểm chung.
6. Vị trí tương đối của mặt cầu và đường
Đối với hình cầu $s\left( o;r \right)$ và đường thẳng $\delta $. Gọi h là hình chiếu đứng của o trên $\delta $, và $d=oh$ là khoảng cách từ o đến $\delta $. Sau đó:
- Nếu $d<r$ thì $\delta $ cắt $s\left( o;r \right)$ tại hai điểm $a,b$ và h là trung điểm của ab.
- Nếu $d=r$ thì $\delta $ và $s\left( o;r \right)$ chỉ có một điểm chung h, trong trường hợp này $\delta $ được gọi là điểm tiếp theo Đường thẳng $s\left( o;r \right)$ hoặc $\delta $ của một hình cầu tiếp tuyến với $s\left( o;r \right)$ và h là tiếp tuyến.
- Nếu $d>r$ thì $\delta $ và $s\left( o;r \right)$ không có điểm chung.
- Diện tích hình cầu: $s=4\pi {{r}^{2}}.$
- Thể tích hình cầu: $v=\frac{4}{3}\pi {{r}^{2}}.$
7.Diện tích của quả bóng và thể tích của quả bóng
Gọi r là bán kính của mặt cầu
8.Một số công thức tính nhanh bán kính đường tròn ngoại tiếp
