Bài tập §8. Các trường hợp đồng dạng của tam giác vuông, Chương 3 – Tam giác đồng dạng, SGK Toán 8, Tập. Nội dung Giải bài 49 50 51 52 trang 84 85 SGK Toán 8 Tập 2 Tổng hợp các công thức, lý thuyết, phương pháp giải bài tập hình học trong SGK Toán 8 giúp học sinh học tốt môn Toán 8 lớp.
Lý thuyết
1. Áp dụng tính đồng dạng của tam giác và tam giác vuông
Hai tam giác vuông bằng nhau nếu:
Góc nhọn của tam giác vuông này bằng tam giác vuông kia.
Tam giác vuông này có hai cạnh tỉ lệ với hai cạnh của tam giác vuông kia.
2. Kí hiệu đặc biệt để nhận biết hai tam giác vuông đồng dạng
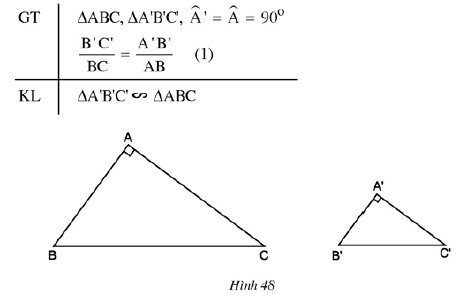
Định lý 1: Hai tam giác vuông bằng nhau nếu cạnh huyền và một cạnh của tam giác vuông kia tỉ lệ với cạnh huyền và một cạnh của tam giác vuông kia.
3. Tỉ số chiều cao, tỉ số diện tích của hai tam giác đồng dạng
Định lý 2: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
Định lý 3: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Dưới đây là hướng dẫn giải bài tập trang 49, 50, 51, 52, 84, 85 Tập 2 SGK Toán 8. Các em vui lòng đọc kỹ câu hỏi trước khi giải bài!
Bài tập
giaibaisgk.com giới thiệu đến các bạn lời giải đầy đủ phần bài tập hình học 8 và lời giải chi tiết 49 50 51 bài 52 trang 84 85 SGK toán 8 tập 2 bài 8. Chương ba là các trường hợp đồng dạng của tam giác vuông – tam giác đồng dạng để các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 49 trang 84 SGK Toán 8 Tập 2
Trong Hình 51, chiều cao của tam giác \(abc\) nằm bên phải của \(a\) là \(ah\)
a) Hình vẽ bên có bao nhiêu cặp tam giác đồng dạng?
b) có nghĩa là: \(ab = 12,45 cm\), \(ac = 20,50cm\). Tính độ dài của các đoạn \(bc, ah, bh\) và \(ch.\)
Giải pháp thay thế:
a)Xét \(∆abc\) và \(∆hba\) có:
\( \widehat{a} = \widehat{h}={90^o}\)
\( \widehat{b}\) chung
\(\rightarrow abc ∽ ∆hba\) (g-g)
Xét \(∆abc\) và \(∆hac\) có:
\( \widehat{a} = \widehat{h}={90^o}\)
\( \widehat{c}\) chung
\(\rightarrow ∆abc ∽ ∆hac\) (g-g)
b) \(∆abc\) là hình vuông tại \(a\) (giả sử) nên áp dụng định lý pitago ta có:
\(\eqalign{ & b{c^2} = a{b^2} + a{c^2} \cr & \;\;\;\; ;\;\;\;= 12,{45^2} + 20,{50^2} = 575,2525 \cr & \rightarrow bc = \sqrt {575,2525} approx 24\,cm \cr} \)
\( abc ∽ ∆hba \) (đã chứng minh ở trên)
\( \rightarrow \dfrac{ab}{hb} = \dfrac{bc}{ba}\)
\( \rightarrow hb = \dfrac{ab^{2}}{bc} ≈ \dfrac{12,45^{2}}{24}≈ 6,5 cm\)
\( \rightarrow ch = bc – bh \khoảng 24 – 6,5 \)\(\,= 17,5 cm.\)
Mặt khác: \( \dfrac{ac}{ah} = \dfrac{bc}{ba}\)
\(\rightarrow ah = \dfrac{ab.ac}{bc} \approx \dfrac{12,45.20,50}{24}\)
\( \rightarrow à \xấp xỉ 10,6 cm\).
2. Giải bài 50 trang 84 SGK Toán 8 Tập 2
Chiều dài bóng của ống khói nhà máy trên mặt đất là \(36,9m\). Cùng lúc đó, một cột sắt cao \(2,1 m\) cắm vuông góc với mặt đất có bóng dài \(1,62m\). Tính chiều cao của ống khói.
Giải pháp thay thế:
Giả sử bàn là \(a’b’\) và bóng của nó là \(a’c’\).
Vì ống khói và thanh sắt vuông góc với mặt đất nên hai tam giác \(abc\) và \(a’b’c’\) là tam giác vuông.
Vì các tia phát ra đồng thời nên ta suy ra \(\widehat {acb} = \widehat {a’c’b’}\)
\( \rightarrow \) hai tam giác vuông \(abc\) và \(a’b’c’\) đồng dạng (hai tam giác vuông có hai góc nhọn bằng nhau)
\( \rightarrow \dfrac{ab}{a’b’} = \dfrac{ac}{a’c’}\) (tính chất của hai tam giác đồng dạng)
\( \rightarrow ab= \dfrac{a’b’.ac}{a’c’}\)
\( \rightarrow ab= \dfrac{2,1.36,9}{1.62}\)
\( \rightarrow ab ≈ 47,8m\).
3. Giải bài 51 tr.84 SGK Toán 8 2
Chiều cao \(ah\) của tam giác vuông \(abc\) chia cạnh huyền \(bc\) thành hai độ dài \(25cm\) và \(36cm) ). Tính chu vi và diện tích tam giác vuông đó (h.53)
Giải thích: Trước tiên hãy tìm \(ah\) từ các tam giác vuông đồng dạng rồi tính các cạnh của tam giác\(abc.\)
Giải pháp thay thế:
\(∆ahb ∽ ∆cha\) (g.g) bởi vì \(\widehat{ahb} = \widehat{ahc}=90^o\) , \(\widehat{bah ) } = \widehat{ach}\) (với \(\widehat {hac}\))
\( \rightarrow \dfrac{ah}{ch }= \dfrac{bh}{ah}\)
\( \rightarrow a{h^2}=ch.bh = 25,36\)
\( \rightarrow a{h^2}= 900 \rightarrow ah = 30cm\)
Vậy \(s_{abc} = \dfrac{1}{2}.ah.bc \)\(\,= \dfrac{1}{2}.30.(25 + 36) = 915 \) cm vuông
Áp dụng py-ta-go vào 2 tam giác vuông \(abh\) và \(ach\) ta được:
\(\begin{array}{l} a{b^2} = b{h^2} + a{h^2}\\ \rightarrow a{b^2} = { 25^2} + {30^2} = 1525\\ \rightarrow ab \khoảng 39,05cm\\ a{c^2} = c{h^2} + a{h^2} \ \rightarrow a{c^2} = {36^2} + {30^2} = 2196\\ \rightarrow ac \xấp xỉ 46,86cm \end{array}\)
Chu vi tam giác abc là: \(p = ab + ac + bc \) \(= 39,05 + 46,86 + 61 = 146,91cm\)
4. Giải bài 51 tr.85 SGK Toán 8 2
Đối với tam giác vuông, độ dài cạnh huyền \(20cm\), và độ dài góc vuông \(12cm\). Tính độ dài hình chiếu của góc vuông còn lại trên cạnh huyền.
Giải pháp thay thế:
\(Δabc\) Chiều cao của hình vuông tại \(a\) là \(ah\), \(bc = 20cm, ab = 12cm\). Chúng tôi tính \(hc\).
Ta có:\(Δabh ∽ Δcbaa\) vì:
\(\widehat b\) trung bình
\( \widehat{h} = \widehat{a}=90^o\)
\( \rightarrow \dfrac{ab}{cb}= \dfrac{bh}{ba}\) (tính chất của hai tam giác đồng dạng)
\( \rightarrow ab^2= hb.cb\)
\( \rightarrow bh = \dfrac{ab^{2}}{cb}= \dfrac{12^{2}}{20} = 7.2 \,(cm)\ )
\( \rightarrow ch = bc – bh = 20 – 7,2 \)\(\,= 12,8\,cm.\)
Trước:
- Giải 46 47 Trang 48 84 SGK Toán 8 Tập 2
- Đáp án bài 53 54 55 trang 87 tập 2 SGK toán 8
- Câu hỏi khác 8
- Học tốt vật lý lớp 8
- Học tốt môn sinh học lớp 8
- Học tốt ngữ văn lớp 8
- Điểm tốt môn lịch sử lớp 8
- Học tốt môn địa lý lớp 8
- Học tốt tiếng Anh lớp 8
- Học tốt môn tiếng Anh lớp 8 thí điểm
- Học Khoa học Máy tính Lớp 8
- Học chăm chỉ môn gdcd lớp 8
Tiếp theo:
Xem thêm:
Chúc các em thành công trong việc soạn Sách Giáo Khoa Toán 8 Có Lời Giải Bài 49 50 51 52 Trang 84 85 SGK Toán 8 Tập 2!
“Môn thể thao nào đã khó giabaisgk.com”
