Bài 67 Trang 102 SGK Toán 8 Tập 1
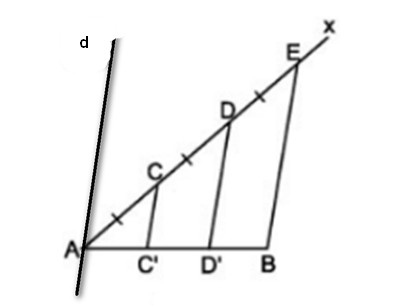
Đối với đoạn thẳng \(ab\). Vẽ tia \(ax\) bất kỳ. Lấy điểm \(c, d, e\) trên tia \(ax\) sao cho \(ac = cd = de\) (h.97). Dòng kẻ \(eb\). Vẽ một đường song song với \(eb\) qua \(c, d\) . Chứng minh rằng đoạn thẳng \(ab\) được chia thành ba phần bằng nhau.
Giải pháp:
Dựng đường thẳng \(d\) song song với \(cc’\) bởi \(a\)
Ta có: \(d//eb // dd’ // cc’\) và \(ac = cd = de\) (giả sử).
Theo định lý đường thẳng song song cách đều ta suy ra đường thẳng \(d,eb,dd’,cc’\) là đường thẳng song song cách đều nên nó cắt các đường thẳng liên tục trên \(ab \) đường thẳng
hoặc \( ac’ = c’d’ = d’b\)
Vì vậy, đoạn \(ab\) được chia thành ba phần.
Bài 68 Trang 102 SGK Toán 8 Tập 1
Cho một điểm \(a\) nằm ngoài đường thẳng \(d\) và cách \(2cm\) so với \(d\). Lấy một điểm \(b\) bất kỳ trên đường thẳng \(d\). Điểm \(c\) được gọi là đối xứng với điểm \(a\) qua điểm \(b\). Điểm \(c\) di chuyển trên đường thẳng nào khi điểm \(b\) di chuyển trên đường thẳng \(d\)?
Giải pháp thay thế:
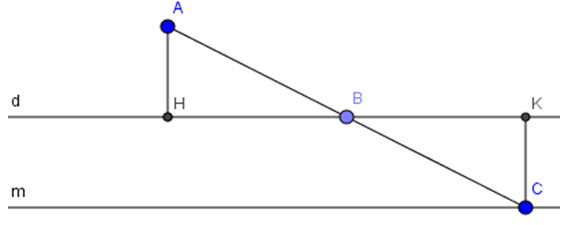
Các đường thẳng \(ah\) và \(ck\) vuông góc với \(d\).
Ta có \(ab = cb\) (vì \(c\) là điểm đối xứng của \(a\) với \(b\))
\(\widehat{abh}\) = \(\widehat{cbk}\) (đối diện)
Vậy \(Δahb = Δckb\)(cường điệu – góc nhọn)
Suy ra\(ck = ah = 2cm\)
Điểm \(c\) cố định cách đường thẳng \(d\)\(2cm\) một khoảng không đổi nên \(c\) nằm trên đường thẳng \ ( m\ ) song song với \(d\) và khoảng cách từ \(d\) bằng \(2cm\).
Bài 69 Trang 103 SGK Toán 8 Tập 1
Nối mỗi ý (1), (2), (3), (4) với một trong các ý (5), (6), (7), (8) để được mệnh đề đúng:
(1) Tập hợp các điểm cách \(a\) \(3cm\)
(2) Tập hợp các điểm cách đều hai đầu của đoạn thẳng \(ab\)
(3) Tập hợp các điểm nằm trong góc \(phép quay\) và cách đều hai cạnh của góc
(4) Tập hợp các điểm cách đều một đường thẳng \(a\) với một khoảng cách cố định \(3cm\)
(5) là đường trung trực của đoạn thẳng \(ab\).
(6) là hai đường thẳng song song với \(a\) và cách nhau bởi \(a\)\(3cm\)
(7) là hình tròn có tâm \(a\) và bán kính \(3cm\).
(8) là tia phân giác của góc \(phép quay\).
Giải pháp thay thế:
Kết hợp các ý tưởng sau:
(1) và (7)
(2) và (5)
(3) và (8)
(4) và (6)
Bài 70 Trang 103 SGK Toán 8 Tập 1
Cho góc \(phép quay\) vuông, điểm \(a\) thuộc tia \(oy\) sao cho \(oa = 2cm\). Lấy \(b\) là một điểm bất kỳ trên tia \(ox\). Gọi \(c\) là trung điểm của \(ab\). Khi điểm \(b\) di chuyển trên tia \(ox\) thì điểm \(c\) di chuyển trên đường nào?
Giải pháp
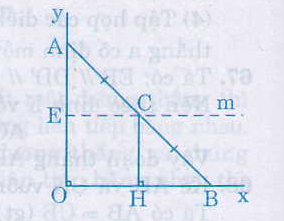
Dòng \(ch ox\)
Ta có \(cb = ca\) (vì \(c\) là trung điểm của \(ab\))
\(ch // ao\) (cùng vuông góc với \(ox\))
Ngược lại \(c\) là trung điểm của \(ab\) nên \(ch\) là đường trung trực của tam giác \(abo\)
Suy ra \(ch = \frac{1}{2}ao = \frac{1}{2}.2 = 1 (cm)\)
Điểm \(c\) cố định cách tia \(ox\)\(1cm\) một khoảng không đổi nên \(c\) nằm trên tia \ (em\) ) song song với \(ox\) và khoảng cách từ \(ox\) bằng \(1cm\).
bài 71 trang 103 SGK Toán 8 tập 1
Tam giác \(abc\) tại \(a\). Lấy \(m\) làm điểm bất kỳ trên cạnh \(bc\). Gọi \(md\) là đường thẳng đứng từ \(m\) đến \(ab\), \(me\) là đường thẳng từ \(m\) đến \(ac ), \(o\) là trung điểm của \(de\).
a) Chứng minh ba điểm\(a, o, m\) thẳng hàng.
b) Khi điểm \(m\) di chuyển trên cạnh \(bc\) thì điểm \(o\) di chuyển trên đường nào?
c) Đâu là điểm \(m\) trên cạnh \(bc\) có độ dài \(am\) nhỏ nhất?
Giải pháp thay thế:
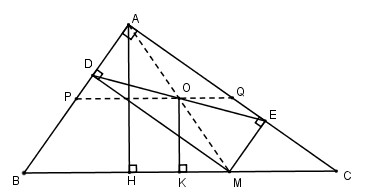
a) tứ giác \(adme\) và \(\widehat a = \widehat d = \widehat e = {90^0}\)
Vậy tứ giác \(adme\) là hình chữ nhật
\(o\) là trung điểm của đường chéo \(de\), nên \(o\) cũng là trung điểm của \(am\).
Căn chỉnh \(a, o, m\)
b) Các bạn \(ah bc\).
Phương pháp 1:
Các bạn \(ok ⊥ bc\). Ta có \(oa = om, ok // ah\) (vì cũng vuông góc với \(bc\)).
Suy ra \(ok = {1 \ trên 2}ah\)
Điểm \(o\) được cố định cách đoạn thẳng \(bc\) một khoảng không đổi bằng \({1 \over 2}ah\).
Mặt khác, khi \(m\) trùng với \(c\) thì \(o\) là trung điểm của \(ac\) và khi \( m \) trùng với \(b\) thì \(o\) là trung điểm của \(ab\).
Vậy \(o\) di chuyển trên đoạn thẳng \(pq\) là đường trung tuyến của tam giác \(abc\).
Phương pháp 2:
Vì \(o\) là trung điểm của \(am\) nên \(ho\) là đường trung bình của cạnh huyền \(am\). Vì vậy \(oa = ồ\). Suy ra rằng điểm \(o\) di chuyển trên đường trung trực của \(ah\).
Ngược lại vì \(m\) di chuyển lên trên \(bc\). Vậy điểm \(o\) di chuyển trên đoạn thẳng \(pq\) là đường trung bình của \(abc\).
c) Ta có \(ah\), là chiều cao từ \(a\) đến \(bc\), nên \(am\ge ah\). Vì vậy \(am\) nhỏ nhất khi \(m\) khớp với \(h\).
bài 72 trang 103 SGK Toán 8 tập 1
Đố vui. Để kẻ một đường thẳng 10cm song song với mép gỗ, người thợ mộc cầm chiếc bút chì cd dài 10cm vuông góc với ngón trỏ (h.98), rồi di ngón trỏ dọc theo mép gỗ ab. Từ những kiến thức nào ta có thể kết luận rằng chì c vẽ một đường thẳng song song và cách ab 10cm?
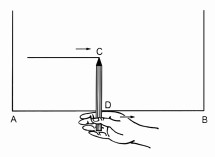
Giải pháp:
Theo tính chất đường thẳng song song với đường thẳng đã cho, ta kết luận do điểm c cách mép gỗ ab 10cm nên đường thẳng đánh dấu bằng chì c song song với ab tại a cách ab 10cm.
giaibaitap.me
