Hướng dẫn giải quyết vấn đề §7. tứ giác nội tiếp. Đo Cung, Chương 3 – Góc Trong Đường Tròn, SGK Toán 9, Tập. Nội dung bài Giải bài 53 54 55 trang 89 SGK Toán 9 Tập 2 tổng hợp các công thức, lý thuyết, phương pháp giải bài tập hình học trong SGK Toán 9 giúp học sinh học tốt môn Toán lớp 9.
Lý thuyết
1. Triết học
Tứ giác có bốn đỉnh nằm trên cùng một đường tròn gọi là tứ giác nội tiếp (hay tứ giác nội tiếp).
2. Định lý
Trong một tứ giác nội tiếp, tổng độ của hai góc đối đỉnh bằng 1800
3. Định lý đảo
Một tứ giác nội tiếp được trong một đường tròn nếu tổng hai góc đối diện của nó bằng 1800.
Sau đây là hướng dẫn trả lời của bài học này để các bạn tham khảo. Vui lòng đọc kỹ câu hỏi trước khi trả lời!
Câu hỏi
1. Trả lời câu 1 Trang 87 SGK Toán 9 Tập 2
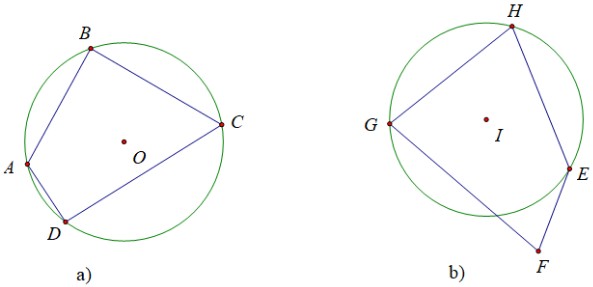
a) Vẽ đường tròn tâm o, rồi vẽ tứ giác có các đỉnh nằm trên đường tròn.
b) Vẽ đường tròn tâm i, sau đó vẽ tứ giác có ba đỉnh nằm trên đường tròn và đỉnh thứ tư không thuộc đường tròn.
Trả lời:
2. Trả lời câu 2 Trang 88 SGK Toán 9 Tập 2
Xem Hình 45 để chứng minh định lý trên.
Trả lời:
Xét đường tròn \((o)\) ta có:
\(\widehat {bad} = \dfrac{1}{2}sđ\,\overparen {bcd}\) (góc nội tiếp chắn \(bcd\))
\(\widehat {bcd} = \dfrac{1}{2}sđ\,\overparen {xấu}\) (góc nội tiếp chắn \(xấu\))
Suy ra\(\widehat {bad} + \widehat {bcd} = \dfrac{1}{2}sđ\,\overparen {bcd} + \dfrac{1}{2 } sđ\,\overparen {xấu} = \dfrac{{sđ\,\overparen {xấu} + sd\,\overparen {bcd}}}{2}\)
\( = \dfrac{{360^\circ }}{2} = 180^\circ .\)
Vậy \(\widehat {bad} + \widehat {bcd} = 180^\circ \) .
Vậy trong một tứ giác nội tiếp, tổng độ của hai góc đối đỉnh là \(180^0\).
Dưới đây là hướng dẫn giải bài 53, 54, 55 trang 89 SGK Toán 2. Các em đọc kỹ câu hỏi trước khi giải nhé!
Bài tập
giaibaisgk.com giới thiệu đến các bạn lời giải phần bài tập Hình học 9 đầy đủ và lời giải chi tiết trang 53 54 55 trang 89 SGK Toán Tập 2 Bài 7. tứ giác nội tiếp. Chương thứ ba là số đo radian – góc với đường tròn để các bạn tham khảo. Chi tiết lời giải của từng bài tập xem bên dưới:
1. Giải bài 53 tr.89 SGK Toán 9 Tập 2
Biết rằng \(abcd\) là tứ giác nội tiếp. Vui lòng điền vào chỗ trống trong biểu mẫu bên dưới (nếu có thể)
Giải pháp:
Theo đề ta có \(abcd\) là tứ giác nội tiếp \( \rightarrow \left\{ \begin{array}{l}\widehat a + \widehat c = { 180^0}\\\widehat b + \widehat d = {180^0}\end{array} \right..\)
♦ Trường hợp 1:
Ta có: \(\widehat a + \widehat c = {180^0}\)
\(\rightarrow \widehat c = {180^0}-\widehat a= {180^0} – {80^0} = {100^0}.\)
\(\widehat b + \widehat d = {180^0} \)
\(\rightarrow \widehat d = {180^0} – \widehat b = {180^0} – {70^0} = {110^0}.\)
Vậy góc còn lại là: \(\widehat{c}= 100^0,\) \(\widehat{d} = 110^0.\)
♦ Trường hợp 2:
\(\begin{array}{l} ta \, \, vâng: \, \, \widehat a + \widehat c = {180^0} \\ rightarrow \widehat a = {180^0} – \widehat c = {180^0} – {105^0} = {75^0}.\\ \widehat b + \widehat d = {180^0}\\ \rightarrow \widehat b = {180^0} – \widehat d = {180^0} – {75^0} = {105^0}. \end{ mảng}\)
♦ Trường hợp 3:
Ta có: \(\widehat a + \widehat c = {180^0} \)
\(\rightarrow \widehat c = {180^0}-\widehat a= {180^0} – {60^0} = {120^0}.\)
là \( \widehat b + \widehat d = {180^0}.\)
Chúng ta có thể chọn \( \widehat b =70^0 \rightarrow \widehat d = {180^0}-70^0=110^0.\)
♦ Trường hợp 4: \(\widehat{d}=180^0-\widehat{b}=180^0 – 40^0= 140^0.\)
Phần còn lại \(\widehat{a}+ \widehat{c}= 180^0.\) Ví dụ: chọn \(\widehat{a}=100^0,\, \widehat {c}=80^0.\)
♦ Trường hợp 5: \(\widehat{a}=180^0-\widehat{c}=180^0-74^0=106^0.\)
\(\widehat{b}= 180^0-\widehat{d}=180^0-65^0=115^0.\)
♦ Trường hợp 6: \(\widehat{c}=180^0-\widehat{a}=180^0-95^0=85^0.\)
\(\widehat{b}=180^0-\widehat{d}=180^0- 98^0=82^0.\)
Hãy điền vào chỗ trống và ta được bảng sau:
2. Giải bài 54 trang 89 SGK Toán 9 Tập 2
Tứ giác \(abcd\) có \(\widehat{abc}+ \widehat{adc}= 180^0\). Chứng minh rằng đường trung trực của \(ac,\, bd, \,ab\) đi qua một điểm.
Giải pháp:
Tứ giác \(abcd\) và \(\widehat{abc}+ \widehat{adc}= 180^0\) có hai góc\(\widehat{abc}\ ) và \( \widehat{adc}\) là hai góc đối đỉnh nên tứ giác \(abcd\) là tứ giác nội tiếp.
Gọi \(o\) là tâm đường tròn ngoại tiếp tứ giác \(abcd\), rồi \(oa=ob=oc=od\)(cùng bán kính của đường tròn ( (o) \) )
+ Vì \(oa = ob\) nên \(o\) thuộc đường phân giác đứng của \(ab\)
+ Vì \(oa = oc\) nên \(o\) là đường thẳng đứng của \(ac\)
+ Vì \(od = ob\) nên \(o\) thuộc đường trung trực của đoạn thẳng \(bd\)
Do đó đường trung trực của \(ab, \, bd, \, ab\) đi qua tâm \(o\) của đường tròn ngoại tiếp tứ giác \(abcd ).
3. Giải bài 55 tr.89 SGK Toán 9 2
Vì \(abcd\) là tứ giác nội tiếp có \(m,\) là tâm nên \(\widehat {dab}= 80^0\), \ ( widehat {dam}= 30^0,\) \(\widehat {bmc}= 70^0\).
Tính số đo của góc\(\widehat {mab},\) \(\widehat {bcm},\) \(\widehat {amb},\) \ ( widehat {dmc},\) \(\widehat {amd},\) \(\widehat {mcd}\) và \(\widehat {bcd}.\)
Giải pháp:
Ta có: \(\widehat {mab} = \widehat {dab} – \widehat {dam} = {80^0} – {30^0} = {50^0}\) (1)
+) \(∆mbc\) là tam giác cân tại \(m\) \((mb= mc)\), nên \(\displaystyle \widehat { bcm} = {{{{180}^0} – {{70}^0}} \trên 2} = {55^0}\) (2)
+) \(∆mab\) là tam giác cân tại \(m\) \((ma=mb)\), nên \(\widehat {mab} = \ widehat {abm} = {50^0}\) (theo (1))
Vậy \(\widehat {amb} = {180^0} – {2.50^0} = {80^0}.\)
Ta có: \(\widehat {bad}=\dfrac{sđ\overparen{bcd}}{2}\) (số đo góc nội tiếp bằng nửa số đo góc bị cắt) .
\(\rightarrow number\overparen{bcd}=2.\widehat {bad} = {2.80^0} = {160^0}.\)
Tức là \(sđ\overparen{bc}= \widehat {bmc} = {70^0}\) (số đo góc ở tâm bằng số đo cung bị chắn).
Vậy \(sđ\overparen{dc}={160^0} – {70^0} = {90^0}\) (vì c nằm trên dải phụ\(bd\) ) .
Suy ra \(\widehat {dmc} = {90^0}.\) (4)
Ta có: \(∆mad\) là tam giác cân tại \(m \) \((ma= md).\)
Suy ra \(\widehat {amd} = {180^0} – {2.30^0}=120^0\) (5)
trong đó \(Δmcd\) nằm trong \(m\) \(((mc= md)\) và \(\widehat {dmc} = {90 ^ 0}\ )
Suy ra \(\widehat {mcd} = \widehat {mdc} = {45^0}.\) (6)
Từ (2) và (6) và do cm là tia nằm giữa hai tia \(cb, \, cd\) nên ta có:
\(\widehat {bcd} =\widehat{bcm}+\widehat{mcd} ={100^0}.\)
Trước:
- Bài tập: Giải bài 48 49 50 51 Trang 52 87 SGK Toán 9 Tập 2
- Bài tập: Giải bài 56 57 58 59 60 trang 89 90 SGK Toán 9 Tập 2
- Câu hỏi khác 9
- Học tốt vật lý lớp 9
- Học tốt môn sinh học lớp 9
- Học tốt ngữ văn lớp 9
- Điểm tốt môn lịch sử lớp 9
- Học tốt môn địa lý lớp 9
- Học tốt tiếng Anh lớp 9
- Tiếng Anh lớp 9 thí điểm
- Học tốt tin học lớp 9
- Học tốt GDCD lớp 9
Tiếp theo:
Xem thêm:
<3
“Bài tập nào khó, đã có giabaisgk.com”
